ಕ್ವಾಡ್ರಾಟಿಕ್ ಮತ್ತು ಘಾತೀಯ ಕಾರ್ಯದ ನಡುವಿನ ವ್ಯತ್ಯಾಸವೇನು? (ವ್ಯತ್ಯಾಸ ವಿವರಿಸಲಾಗಿದೆ) - ಎಲ್ಲಾ ವ್ಯತ್ಯಾಸಗಳು
ಪರಿವಿಡಿ
ನೀವು 9ನೇ ಅಥವಾ 11ನೇ ತರಗತಿಯಲ್ಲಿ ನಿಮ್ಮ ಪಠ್ಯಕ್ರಮದ ಭಾಗವಾಗಿ ಕ್ವಾಡ್ರಾಟಿಕ್ ಮತ್ತು ಎಕ್ಸ್ಪೋನೆನ್ಷಿಯಲ್ ಫಂಕ್ಷನ್ಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡಿರಬಹುದು. ಆದಾಗ್ಯೂ, ನಿಮ್ಮ ಪಠ್ಯಕ್ರಮದ ಭಾಗವಾಗಿ ಈ ಕಾರ್ಯಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡುವುದು ನಿಮಗೆ ಎರಡರ ನಡುವಿನ ವ್ಯತ್ಯಾಸದ ಸ್ಪಷ್ಟ ತಿಳುವಳಿಕೆಯನ್ನು ನೀಡುವುದಿಲ್ಲ.
ನಿಮ್ಮ ಪಠ್ಯಕ್ರಮದ ಭಾಗವಾಗಿ, ಎರಡಕ್ಕೂ ಮತ್ತು ಅವುಗಳ ಅನ್ವಯಗಳ ನಡುವಿನ ಸಂಭವನೀಯ ವ್ಯತ್ಯಾಸಗಳ ಬಗ್ಗೆ ಎಂದಿಗೂ ಊಹೆ ಮಾಡದೆಯೇ ನೀವು ಸಮೀಕರಣಗಳು ಮತ್ತು ಎರಡಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸುವ ಅಗತ್ಯವಿದೆ.
ಆದ್ದರಿಂದ ಈ ಲೇಖನದಲ್ಲಿ, ಗ್ರಾಫ್ಗಳು, ಸಮೀಕರಣಗಳು ಮತ್ತು ಉದಾಹರಣೆಗಳ ಸಹಾಯದಿಂದ ಎರಡರ ನಡುವಿನ ವ್ಯತ್ಯಾಸವನ್ನು ನಾನು ನಿಮಗೆ ತಿಳಿಸುವ ಗುರಿಯನ್ನು ಹೊಂದಿದ್ದೇನೆ ಇದರಿಂದ ನೀವು ಜ್ಞಾನವನ್ನು ಸುಲಭವಾಗಿ ಗ್ರಹಿಸಬಹುದು.
ಪ್ರಾರಂಭಿಸೋಣ.
ಗಣಿತದಲ್ಲಿ ಕಾರ್ಯ ಎಂದರೇನು?
ಗಣಿತದಲ್ಲಿ ಒಂದು ಕಾರ್ಯವನ್ನು ಇನ್ಪುಟ್ಗಳ ನಡುವಿನ ಸಂಬಂಧವಾಗಿ ಉತ್ತಮವಾಗಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ, ಅಲ್ಲಿ ಪ್ರತಿ ಇನ್ಪುಟ್ ಒಂದೇ ಫಲಿತಾಂಶವನ್ನು ಹೊಂದಿರುತ್ತದೆ ಅಂದರೆ ಪ್ರತಿ ಇನ್ಪುಟ್ ಒಂದೇ ಔಟ್ಪುಟ್ ಅನ್ನು ಹಿಂತಿರುಗಿಸುತ್ತದೆ.
ಗಣಿತದಲ್ಲಿನ ಕಾರ್ಯವನ್ನು ಸಾಮಾನ್ಯವಾಗಿ f(x) ನಿಂದ ತೋರಿಸಲಾಗುತ್ತದೆ ಅಥವಾ ಪ್ರತಿನಿಧಿಸಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ f(x)=x^2. ಈ ಕಾರ್ಯವು ನಮಗೆ ಬ್ರಾಕೆಟ್ನಲ್ಲಿನ ಸಂಖ್ಯೆಯ ವರ್ಗವನ್ನು ನೀಡುತ್ತದೆ, ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಸಂಖ್ಯೆ 2.
ಇದು ಫಂಕ್ಷನ್ನಲ್ಲಿನ ಇನ್ಪುಟ್ ಏನೇ ಇರಲಿ ನಮಗೆ ಅದೇ ಔಟ್ಪುಟ್ ನೀಡುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಇದು ಯಾವಾಗಲೂ ಬ್ರಾಕೆಟ್ನಲ್ಲಿರುವ ಸಂಖ್ಯೆಯ ವರ್ಗವನ್ನು ಔಟ್ಪುಟ್ ಆಗಿ ಹಿಂತಿರುಗಿಸುತ್ತದೆ.
ಗಣಿತದಲ್ಲಿ ಹಲವಾರು ಕಾರ್ಯಗಳನ್ನು ವಿವಿಧ ಕಾರ್ಯಗಳನ್ನು ಸಾಧಿಸಲು ಬಳಸಲಾಗುತ್ತದೆ ಮತ್ತು ಅವುಗಳನ್ನು ವಿವಿಧ ಪ್ರದೇಶಗಳಲ್ಲಿ ಅನ್ವಯಿಸಲಾಗುತ್ತದೆ. ಆದಾಗ್ಯೂ, ನಾವು ಚರ್ಚಿಸಲಿರುವ ಕಾರ್ಯಗಳುಈ ಲೇಖನದಲ್ಲಿ ಚತುರ್ಭುಜ ಮತ್ತು ಘಾತೀಯ ಕಾರ್ಯಗಳಾಗಿವೆ. ಈ ಎರಡು ಕಾರ್ಯಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸವನ್ನು ಹೈಲೈಟ್ ಮಾಡಲು ನಾವು ಮುಖ್ಯವಾಗಿ ಗಮನಹರಿಸುತ್ತೇವೆ.
ಕ್ವಾಡ್ರಾಟಿಕ್ ಫಂಕ್ಷನ್ ಎಂದರೇನು?
ಒಂದು ಕ್ವಾಡ್ರಾಟಿಕ್ ಫಂಕ್ಷನ್ ಬಹುಪದೀಯ ಕಾರ್ಯವಾಗಿದೆ ಮತ್ತು ಇದು ax^2+bx+c ಸಮೀಕರಣದ ಯಾವುದೇ ರೂಪವಾಗಿದೆ. ಇದನ್ನು ಡಿಗ್ರಿ 2 ರ ಬಹುಪದೋಕ್ತಿ ಎಂದೂ ಕರೆಯುತ್ತಾರೆ ಏಕೆಂದರೆ ಗರಿಷ್ಠ ಘಾತ 2 ಆಗಿರಬಹುದು.
ಚತುರ್ಭುಜ ಸೂತ್ರವನ್ನು ಎಂಜಿನಿಯರಿಂಗ್ನಂತಹ ವಿಜ್ಞಾನದ ವಿವಿಧ ಕ್ಷೇತ್ರಗಳಲ್ಲಿ ಬಳಸಲಾಗುತ್ತದೆ. ಇದನ್ನು ಪ್ಯಾರಾಬೋಲಾ ಮೂಲಕ ಚಿತ್ರಾತ್ಮಕವಾಗಿ ನಿರೂಪಿಸಲಾಗಿದೆ.
ನಮ್ಮ ದೈನಂದಿನ ಜೀವನದಲ್ಲಿ ಚೆಂಡನ್ನು ಎಸೆಯುವುದು ಅಥವಾ ಗಾಲ್ಫ್ ಚೆಂಡನ್ನು ಹೊಡೆಯುವಂತಹ ವಿಭಿನ್ನ ಚಟುವಟಿಕೆಗಳಿಗೆ ಈ ಪ್ಯಾರಾಬೋಲಾವನ್ನು ಬಳಸಲಾಗುತ್ತದೆ. ಮಾಪನಗಳಲ್ಲಿ ಕಾಣೆಯಾದ ಅಸ್ಥಿರಗಳನ್ನು ಕಂಡುಹಿಡಿಯಲು ಮತ್ತು ಯಾವುದೇ ವಸ್ತುವಿನ ವೇಗವನ್ನು ಕಂಡುಹಿಡಿಯಲು ಮತ್ತು ವಾಣಿಜ್ಯ ಕ್ಷೇತ್ರದಲ್ಲಿ ಯಾವುದೇ ಐಟಂ ಅಥವಾ ಉತ್ಪನ್ನದ ಲಾಭವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಚತುರ್ಭುಜ ಸಮೀಕರಣಗಳನ್ನು ಸಹ ಬಳಸಲಾಗುತ್ತದೆ.
ಚತುರ್ಭುಜ ಸಮೀಕರಣದ ಉದಾಹರಣೆ ಇಲ್ಲಿದೆ: 3x^ 2+5x+9 a:3 b:5 c:9
ಸಹ ನೋಡಿ: "ಕನಸು" ಮತ್ತು "ಕನಸು" ನಡುವಿನ ವ್ಯತ್ಯಾಸವೇನು? (ನಾವು ಕಂಡುಹಿಡಿಯೋಣ) - ಎಲ್ಲಾ ವ್ಯತ್ಯಾಸಗಳುಇದು ಅದರ ಪ್ರಮಾಣಿತ ರೂಪದಲ್ಲಿ ಕ್ವಾಡ್ರಾಟಿಕ್ ಫಂಕ್ಷನ್ಗೆ ಉದಾಹರಣೆಯಾಗಿದೆ. ಅಂತಹ ಸಮೀಕರಣಗಳನ್ನು ಪರಿಹರಿಸಲು ಬಳಸುವ ಸೂತ್ರವನ್ನು ಕ್ವಾಡ್ರಾಟಿಕ್ ಫಾರ್ಮುಲಾ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಅದು ಈ ಕೆಳಗಿನಂತಿರುತ್ತದೆ: (-b±√(b²-4ac))/(2a).
ಘಾತೀಯ ಕಾರ್ಯ ಎಂದರೇನು?
ಗಣಿತದಲ್ಲಿ ಘಾತೀಯ ಕಾರ್ಯವು f(x)=a^x ರೂಪದಲ್ಲಿರುವ ಒಂದು ಕಾರ್ಯವಾಗಿದೆ, ಅಲ್ಲಿ a ಆಧಾರವಾಗಿದೆ, ಇದು ಸ್ಥಿರವಾಗಿರುತ್ತದೆ ಮತ್ತು ಅದು ಯಾವಾಗಲೂ 0 ಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿರಬೇಕು. f(x)=\exp ಅಥವಾ e^{x} ನಿಂದ ಸೂಚಿಸಲಾಗಿದೆ.
ಹೆಚ್ಚು ವ್ಯಾಪಕವಾಗಿ ಬಳಸಲಾಗುವ ಘಾತೀಯ ಬೇಸ್ ಬೇಸ್ e ಆಗಿದೆ ಇದನ್ನು ನೈಸರ್ಗಿಕ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆಲಾಗರಿಥಮ್. ಜನಸಂಖ್ಯೆ ಮತ್ತು ಬ್ಯಾಕ್ಟೀರಿಯಾದಂತಹ ವಿವಿಧ ವಸ್ತುಗಳ ಬೆಳವಣಿಗೆಯ ದರವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಇದನ್ನು ಬಳಸಲಾಗುತ್ತದೆ. ಘಾತೀಯ ಕಾರ್ಯವು ಗಣಿತದಲ್ಲಿ ವಾದಯೋಗ್ಯವಾಗಿ ಅತ್ಯಂತ ಪ್ರಮುಖವಾದ ಕಾರ್ಯವಾಗಿದೆ.
ಇದು ಬಹಳ ಮುಖ್ಯ ಏಕೆಂದರೆ ಇದನ್ನು ವಿವಿಧ ಕ್ಷೇತ್ರಗಳಲ್ಲಿ ಬಳಸಲಾಗುತ್ತದೆ:
- ವಿಜ್ಞಾನ
- ವಾಣಿಜ್ಯ.
ಉದಾಹರಣೆಗೆ, ನೀವು ಬ್ಯಾಂಕಿನಲ್ಲಿ ಠೇವಣಿ ಮಾಡುವ ಹಣದ ಮೇಲಿನ ಬಡ್ಡಿ ದರವು ಘಾತೀಯವಾಗಿ ಹೆಚ್ಚಾಗುತ್ತದೆ ಅಂದರೆ ಅದು ಘಾತೀಯ ಕರ್ವ್ ಅನ್ನು ಅನುಸರಿಸುತ್ತದೆ, ಘಾತೀಯ ಕಾರ್ಯಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಅದನ್ನು ಲೆಕ್ಕಹಾಕಬಹುದು.
ಇದಲ್ಲದೆ, ಸಾಲದ ಬೆಳವಣಿಗೆಯು ಘಾತೀಯವಾಗಿ ಹೆಚ್ಚಾಗುತ್ತದೆ ಮತ್ತು ಘಾತೀಯ ಕರ್ವ್ ಅನ್ನು ಅನುಸರಿಸುತ್ತದೆ, ಆದ್ದರಿಂದ, ಘಾತೀಯ ಕಾರ್ಯಗಳನ್ನು ಬಳಸುವುದರ ಮೂಲಕ ನಿಮ್ಮ ಸಾಲವನ್ನು ಹೆಚ್ಚಿಸುವುದನ್ನು ನಿಲ್ಲಿಸಬಹುದು ಮತ್ತು ನಿಮ್ಮ ಹಣಕಾಸಿನ ಮೇಲೆ ಹೆಚ್ಚಿನ ನಿಯಂತ್ರಣವನ್ನು ಹೊಂದಬಹುದು.
ಜೀವಶಾಸ್ತ್ರದಲ್ಲಿ, ನಿರ್ದಿಷ್ಟ ಅವಧಿಯಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಪ್ರದೇಶದ ಜನಸಂಖ್ಯೆಯ ಬೆಳವಣಿಗೆಯನ್ನು ಅಂದಾಜು ಮಾಡಲು ಇದನ್ನು ಬಳಸಲಾಗುತ್ತದೆ.
ಯುರೇನಿಯಂನ ಕೊಳೆಯುವಿಕೆಯಂತಹ ವಿಕಿರಣಶೀಲತೆಯು ಘಾತೀಯ ಬೆಳವಣಿಗೆಯನ್ನು ಅನುಸರಿಸುತ್ತದೆ. ಹೀಗಾಗಿ, ಇದು ಘಾತೀಯ ಕ್ರಿಯೆಯ ಮತ್ತೊಂದು ಅನ್ವಯವಾಗಿದೆ.
ಭೌತಶಾಸ್ತ್ರದಲ್ಲಿ, ಪಾಪ, ಕಾಸ್, ಧ್ವನಿ ತರಂಗಗಳು ಮತ್ತು ಇತರ ಅನೇಕ ತರಂಗಗಳಂತಹ ಎಲ್ಲಾ ತರಂಗಗಳನ್ನು ಘಾತೀಯ ಕಾರ್ಯಗಳ ವಿಷಯದಲ್ಲಿ ಬರೆಯಬಹುದು ಆದ್ದರಿಂದ ಈ ಕಾರ್ಯವು ಭೌತವಿಜ್ಞಾನಿಗಳಿಗೆ ಈ ತರಂಗಗಳನ್ನು ಸಂಶೋಧಿಸಲು ಸಹಾಯ ಮಾಡುತ್ತದೆ.
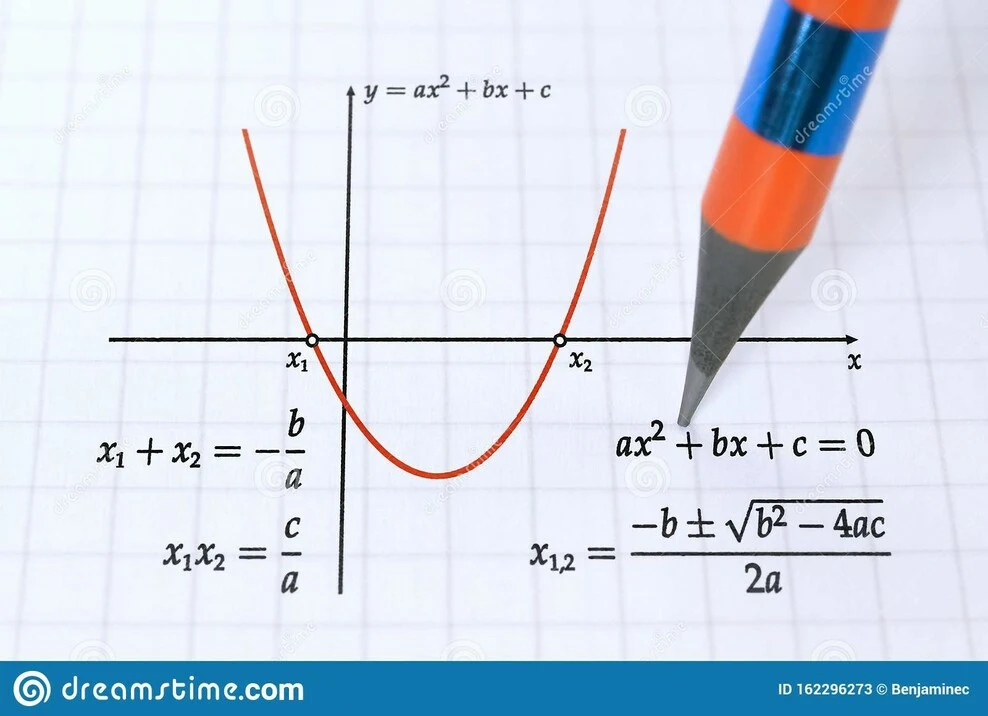
ಏನು ಕ್ವಾಡ್ರಾಟಿಕ್ ಗ್ರಾಫ್ ಆಗಿದೆಯೇ?

ಇದು ಕ್ವಾಡ್ರಾಟಿಕ್ ಗ್ರಾಫ್ನ ಪ್ರಾತಿನಿಧ್ಯವಾಗಿದೆ
ಮೇಲಿನ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಕ್ವಾಡ್ರಾಟಿಕ್ ಫಂಕ್ಷನ್ನ ಗ್ರಾಫ್ ಯು-ಆಕಾರದ ಪ್ಯಾರಾಬೋಲಾ ಆಗಿದೆ. ಈ ಪ್ಯಾರಾಬೋಲಾವು ನಗುವಿನಂತೆ ತೆರೆದುಕೊಳ್ಳಬಹುದು ಅಥವಾ ಗಂಟಿಕ್ಕಿದಂತೆ ಕೆಳಮುಖವಾಗಿ ತೆರೆಯಬಹುದು. ದಿಪ್ಯಾರಾಬೋಲಾ ತೆರೆಯುವ ವಿಧಾನವು ಗುಣಾಂಕದ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ: "a" ಸಮೀಕರಣದ ax^2+bx+c. ಗುಣಾಂಕವು a>0 ಆಗಿದ್ದರೆ ಪ್ಯಾರಾಬೋಲಾ ತೆರೆದುಕೊಳ್ಳುತ್ತದೆ ಮತ್ತು ಗುಣಾಂಕ a<0 ಆಗಿದ್ದರೆ ಪ್ಯಾರಾಬೋಲಾ ಕೆಳಗೆ ತೆರೆಯುತ್ತದೆ.
- ಪ್ಯಾರಾಬೋಲಾದ ಅತ್ಯುನ್ನತ ಅಥವಾ ಕಡಿಮೆ ಬಿಂದುವನ್ನು ಶೃಂಗ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
- ಶೃಂಗವು ಪ್ರತಿನಿಧಿಸುವ ಬಿಂದು, ಗರಿಷ್ಠ ಅಥವಾ ಕನಿಷ್ಠವು ಪ್ಯಾರಾಬೋಲಾ ತೆರೆಯುವ ವಿಧಾನವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.
ಅದು ತೆರೆದರೆ, ಶೃಂಗವು ಗ್ರಾಫ್ನಲ್ಲಿ ಕನಿಷ್ಠ ಬಿಂದುವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ ಮತ್ತು ಅದು ಇದ್ದರೆ ಕೆಳಗೆ ತೆರೆಯುತ್ತದೆ ನಂತರ ಶೃಂಗವು ಕ್ವಾಡ್ರಾಟಿಕ್ ಗ್ರಾಫ್ನಲ್ಲಿ ಗರಿಷ್ಠ ಬಿಂದುವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ. ಪ್ಯಾರಾಬೋಲಾಗಳ ಮತ್ತೊಂದು ವೈಶಿಷ್ಟ್ಯವೆಂದರೆ ಸಮ್ಮಿತಿಯ ರೇಖೆಯು ಶೃಂಗದ ಮೂಲಕ ಹಾದುಹೋಗುವ ಲಂಬ ರೇಖೆಯಾಗಿದೆ ಮತ್ತು ಪ್ಯಾರಾಬೋಲಾವನ್ನು 2 ಸಮಾನ ಮತ್ತು ಒಂದೇ ಭಾಗಗಳಾಗಿ ವಿಭಜಿಸಲು ಬಳಸಲಾಗುತ್ತದೆ.
ಕೆಳಗಿನ ಸೂತ್ರವನ್ನು ಬಳಸಿಕೊಂಡು ಇದನ್ನು ಪಡೆಯಬಹುದು: y =a(x-h)2+k. ಕ್ವಾಡ್ರಾಟಿಕ್ ಗ್ರಾಫ್ ವೈ-ಇಂಟರ್ಸೆಪ್ಟ್ ಅನ್ನು ಹೊಂದಿದೆ, ಇದು ಪ್ಯಾರಾಬೋಲಾ ವೈ-ಅಕ್ಷವನ್ನು ಛೇದಿಸುವ ಬಿಂದುವಾಗಿದೆ. ಈ y-ಪ್ರತಿಬಂಧವು ಕೇವಲ ಒಂದು ಮೌಲ್ಯವನ್ನು ಹೊಂದಿದೆ ಅಂದರೆ ಪ್ಯಾರಾಬೋಲಾ y ಅಕ್ಷವನ್ನು ಒಮ್ಮೆ ಮಾತ್ರ ಛೇದಿಸುತ್ತದೆ. x-ಇಂಟರ್ಸೆಪ್ಟ್ ಎಂಬುದು ಪ್ಯಾರಾಬೋಲಾ x-ಅಕ್ಷವನ್ನು ಪ್ರತಿಬಂಧಿಸುವ ಅಥವಾ ದಾಟುವ ಬಿಂದುವಾಗಿದೆ.
ಪ್ರತಿಬಂಧಗಳ ಸಂಖ್ಯೆಯು 0, 1, ಅಥವಾ 2 ಆಗಿರಬಹುದು. ಗರಿಷ್ಠ ಸಂಖ್ಯೆಯ ಪ್ರತಿಬಂಧಕಗಳು 2 ಆಗಿರಬಹುದು ಏಕೆಂದರೆ ಒಂದು ಚತುರ್ಭುಜ ಸಮೀಕರಣವು ಕೇವಲ 2 ಪರಿಹಾರಗಳು ಅಥವಾ 2 ಬೇರುಗಳನ್ನು ಹೊಂದಿರುತ್ತವೆ. ಕ್ವಾಡ್ರಾಟಿಕ್ ಗ್ರಾಫ್ ಚತುರ್ಭುಜ ಸಮೀಕರಣಗಳನ್ನು ಪರಿಹರಿಸುವ ಒಂದು ಮಾರ್ಗವಾಗಿದೆ. ಇದನ್ನು ಕ್ವಾಡ್ರಾಟಿಕ್ ಸಮೀಕರಣಗಳನ್ನು ಪರಿಹರಿಸುವ ಚಿತ್ರಾತ್ಮಕ ವಿಧಾನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.
ಕ್ವಾಡ್ರಾಟಿಕ್ ಗ್ರಾಫ್ ಅನ್ನು ಬಳಸಲಾಗುತ್ತದೆನಮ್ಮ ದೈನಂದಿನ ಜೀವನದ ಅನೇಕ ಕ್ಷೇತ್ರಗಳು ಮುಖ್ಯವಾಗಿ ಕ್ರೀಡೆಗಳಲ್ಲಿ. ಚೆಂಡನ್ನು ಎಸೆಯುವುದು ಅಥವಾ ಎತ್ತರದ ವೇದಿಕೆಯಿಂದ ಜಿಗಿಯುವುದು, ಕ್ವಾಡ್ರಾಟಿಕ್ ಗ್ರಾಫ್ ಮೂಲಕ ಪ್ರದರ್ಶಿಸಬಹುದಾದ ಸಂದರ್ಭಗಳ ಉದಾಹರಣೆಗಳಾಗಿವೆ. ಚೆಂಡನ್ನು ಅಥವಾ ವ್ಯಕ್ತಿಯು ತಲುಪಿದ ಗರಿಷ್ಠ ಅಥವಾ ಕನಿಷ್ಠ ಅಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಲು ಚತುರ್ಭುಜ ಗ್ರಾಫ್ ಅನ್ನು ನಂತರ ಬಳಸಬಹುದು.
ಘಾತೀಯ ಗ್ರಾಫ್ಗಳು ಯಾವುವು?
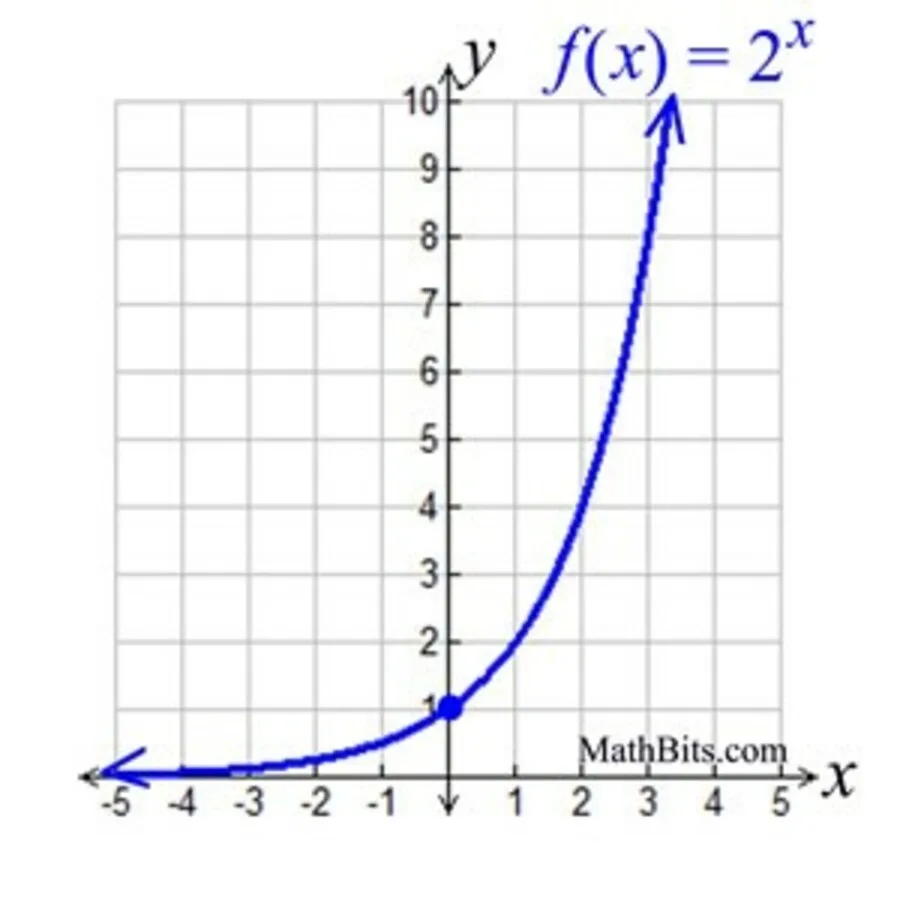
ಇದು ಘಾತೀಯ ಗ್ರಾಫ್ನ ಪ್ರಾತಿನಿಧ್ಯವಾಗಿದೆ
ಬೀಜಗಣಿತ ಮತ್ತು ಅತೀಂದ್ರಿಯ ಸಮೀಕರಣಗಳೆರಡನ್ನೂ ಸಾಮಾನ್ಯವಾಗಿ ಕ್ಯಾಲ್ಕುಲೇಟರ್ನ ಸಹಾಯದಿಂದ ಕೈಯಿಂದ ಪರಿಹರಿಸಬಹುದು, ಆದಾಗ್ಯೂ, ಈ ಎರಡು ಸಮೀಕರಣಗಳು, ಬೀಜಗಣಿತ ಮತ್ತು ಅತೀಂದ್ರಿಯವು ಒಟ್ಟಿಗೆ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತದೆ, ಅವುಗಳನ್ನು ಕೈಯಿಂದ ಪರಿಹರಿಸುವುದು ತುಂಬಾ ಕಷ್ಟ ಅಥವಾ ಅಸಾಧ್ಯವಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ ಈ ಎರಡು ಸಮೀಕರಣಗಳನ್ನು ಒಟ್ಟಿಗೆ ಪರಿಹರಿಸಲು, ನಾವು ಘಾತೀಯ ಗ್ರಾಫ್ ಅನ್ನು ಬಳಸುತ್ತೇವೆ ಮತ್ತು ಅದನ್ನು ಚಿತ್ರಾತ್ಮಕವಾಗಿ ಪರಿಹರಿಸುತ್ತೇವೆ.
ಸರಳವಾದ ಘಾತೀಯ ಕಾರ್ಯವೆಂದರೆ f(x) = ax, a>0, a≠1. ಈ ಕಾರ್ಯದಲ್ಲಿ, ಆಧಾರವು ಯಾವಾಗಲೂ 0 ಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ ಏಕೆಂದರೆ ಬೇಸ್ 0 ಗಿಂತ ಕಡಿಮೆಯಿದ್ದರೆ ಅದು ನಮಗೆ ಅವಾಸ್ತವ ಸಂಖ್ಯೆಯನ್ನು ನೀಡುತ್ತದೆ.
ಬೇಸ್ 1 ಆಗಿದ್ದರೆ ಅದು ಯಾವಾಗಲೂ 1 ಅನ್ನು ಅದರ ಘಾತವನ್ನು ಲೆಕ್ಕಿಸದೆ ಹಿಂತಿರುಗಿಸುತ್ತದೆ ಮತ್ತು ಅದು ತುಂಬಾ ನೀರಸ ಕಾರ್ಯವಾಗಿ ಹೊರಹೊಮ್ಮುತ್ತದೆ. ಈ ಕಾರಣಗಳಿಂದಾಗಿ ಘಾತೀಯ ಕಾರ್ಯದ ಮೇಲೆ ಕೆಲವು ನಿರ್ಬಂಧಗಳನ್ನು ಇರಿಸಲಾಗಿದೆ.
ಸಹ ನೋಡಿ: ಮನ್ಹುವಾ ಮಂಗಾ ವಿರುದ್ಧ ಮನ್ಹ್ವಾ (ಸುಲಭವಾಗಿ ವಿವರಿಸಲಾಗಿದೆ) - ಎಲ್ಲಾ ವ್ಯತ್ಯಾಸಗಳುಘಾತೀಯ ಕ್ರಿಯೆಯ ಗ್ರಾಫ್ ಬೇಸ್ 1 ಕ್ಕಿಂತ ಹೆಚ್ಚಿದೆಯೇ ಅಥವಾ 1 ಕ್ಕಿಂತ ಕಡಿಮೆ ಆದರೆ 0 ಕ್ಕಿಂತ ಹೆಚ್ಚಿದೆಯೇ ಎಂಬುದನ್ನು ಅವಲಂಬಿಸಿ ವಿಭಿನ್ನ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಪ್ರದರ್ಶಿಸುತ್ತದೆ. ಬೇಸ್ ಮಾಡಿದಾಗ ಈ ಕೆಳಗಿನ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಪ್ರದರ್ಶಿಸಿ1 ಕ್ಕಿಂತ ದೊಡ್ಡದಾಗಿರುತ್ತದೆ. ಡೊಮೇನ್ ನೈಜ ಸಂಖ್ಯೆಗಳನ್ನು ಮಾತ್ರ ಒಳಗೊಂಡಿರುತ್ತದೆ, ಶ್ರೇಣಿಯು y>0 ಆಗಿರುತ್ತದೆ, ಗ್ರಾಫ್ ನಿರಂತರವಾಗಿ ಹೆಚ್ಚಾಗುತ್ತದೆ, ಗ್ರಾಫ್ ನಿರಂತರವಾಗಿರುತ್ತದೆ ಮತ್ತು ಅದು ಮೃದುವಾಗಿರುತ್ತದೆ.
ಘಾತೀಯ ಗ್ರಾಫ್ ಇದೇ ರೀತಿ ತೋರಿಸುತ್ತದೆ ಮೂಲವು 1 ಕ್ಕಿಂತ ಕಡಿಮೆ ಆದರೆ 0 ಕ್ಕಿಂತ ದೊಡ್ಡದಾಗಿದ್ದರೆ ಗುಣಲಕ್ಷಣಗಳು. ಅದರ ಗುಣಲಕ್ಷಣಗಳಲ್ಲಿನ ಬದಲಾವಣೆಯೆಂದರೆ ಗ್ರಾಫ್ ಕಡಿಮೆಯಾಗುವುದು. ಘಾತೀಯ ಕಾರ್ಯಗಳ ಮೂಲಕ ಪಡೆದ ಡೇಟಾವನ್ನು ಪ್ರತಿನಿಧಿಸಲು ಘಾತೀಯ ಗ್ರಾಫ್ಗಳನ್ನು ಬಳಸಲಾಗುತ್ತದೆ. ಡೇಟಾದ ಪ್ರಕಾರಗಳು ಮತ್ತು ಘಾತೀಯ ಕಾರ್ಯಗಳ ಅನ್ವಯವನ್ನು ಈ ಹಿಂದೆ ಚರ್ಚಿಸಲಾಗಿದೆ.
ಘಾತೀಯ ಮತ್ತು ಕ್ವಾಡ್ರಾಟಿಕ್ ಕಾರ್ಯಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸ (ಇಲ್ಲಿ ವಿಷಯವನ್ನು ಟೇಬಲ್ ಆಗಿ ಬಳಸಿ)
ಈಗ ಕ್ವಾಡ್ರಾಟಿಕ್ ಮತ್ತು ಘಾತೀಯ ಕಾರ್ಯಗಳನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಲಾಗಿದೆ ಈ ಎರಡು ಪ್ರಮುಖ ಕಾರ್ಯಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸವನ್ನು ನಾವು ಚರ್ಚಿಸುತ್ತೇವೆ.
| ಕ್ವಾಡ್ರಾಟಿಕ್ ಫಂಕ್ಷನ್ | ಘಾತೀಯ ಕಾರ್ಯ | ವೇರಿಯೇಬಲ್ ಆಧಾರವಾಗಿದೆ ಮತ್ತು ಹೆಚ್ಚಿನ ಸಂಭವನೀಯ ಶಕ್ತಿಯು (ax^2+bx+c) ಆಗಿದೆ. | ಬೇಸ್ ಸ್ಥಿರವಾಗಿರುತ್ತದೆ ಮತ್ತು ಆ ಬೇಸ್ನ ಶಕ್ತಿಯು ವೇರಿಯಬಲ್ ಆಗಿದೆ. |
|---|---|
| ಬದಲಾವಣೆಯ ದರವು ಸ್ಥಿರವಾಗಿರುತ್ತದೆ ಅಂದರೆ ಗ್ರಾಫ್ ಸ್ಥಿರ ದರದಲ್ಲಿ ಹೆಚ್ಚಾಗುತ್ತದೆ ಮತ್ತು ಆದ್ದರಿಂದ ನಿರ್ದಿಷ್ಟ ಸಮಯದ ಅವಧಿಯಲ್ಲಿ ಗ್ರಾಫ್ನಲ್ಲಿನ ಬದಲಾವಣೆಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವುದು ಸುಲಭ. | ಒಂದು ಘಾತೀಯ ಕಾರ್ಯ, ಬದಲಾವಣೆಯ ದರವು ಸ್ವತಃ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ ಮತ್ತು ಗ್ರಾಫ್ ಹೆಚ್ಚುತ್ತಿರುವ ದರದಲ್ಲಿ ಹೆಚ್ಚಾಗುತ್ತದೆ. |
| ಕ್ವಾಡ್ರಾಟಿಕ್ ಗ್ರಾಫ್ ಅನ್ನು ರೂಪಿಸುತ್ತದೆಮೇಲ್ಮುಖವಾಗಿ ಅಥವಾ ಕೆಳಮುಖವಾಗಿ ಶೃಂಗವನ್ನು ತಲುಪಿದಾಗ ಪ್ಯಾರಾಬೋಲಾ ಅದು ತನ್ನ ಗರಿಷ್ಠ ಅಥವಾ ಕನಿಷ್ಠ ಬಿಂದುವನ್ನು ತಲುಪಿದಾಗ. | ಘಾತೀಯ ಗ್ರಾಫ್ ಮೊದಲಿನಿಂದಲೂ ವಕ್ರವಾಗಿ ಮುಂದುವರಿಯುತ್ತದೆ. |
ಕ್ವಾಡ್ರಾಟಿಕ್ ಫಂಕ್ಷನ್ ವಿರುದ್ಧ ಘಾತೀಯ ಫಂಕ್ಷನ್
ತೀರ್ಮಾನ
ಎರಡರ ನಡುವಿನ ವ್ಯತ್ಯಾಸವನ್ನು ಸಂಪೂರ್ಣವಾಗಿ ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲು ಸಂಕ್ಷಿಪ್ತ ವಿವರಣೆ
ಒಟ್ಟಾರೆಯಾಗಿ ಹೇಳುವುದಾದರೆ, ಕ್ವಾಡ್ರಾಟಿಕ್ ಫಂಕ್ಷನ್ಗಳು ಮತ್ತು ಎಕ್ಸ್ಪೋನೆನ್ಷಿಯಲ್ ಫಂಕ್ಷನ್ಗಳು ಅವುಗಳ ಅನ್ವಯ ಮತ್ತು ಅವುಗಳ ಪರಿಕಲ್ಪನೆಯಲ್ಲಿ ಪರಸ್ಪರ ಭಿನ್ನವಾಗಿರುತ್ತವೆ. ಘಾತೀಯ ಕಾರ್ಯವು ನಿರಂತರ ಹೆಚ್ಚಳವನ್ನು ಸೂಚಿಸುತ್ತದೆ ಆದರೆ ಚತುರ್ಭುಜ ಕಾರ್ಯವು ಹೆಚ್ಚಳ ಮತ್ತು ಇಳಿಕೆ ಎರಡನ್ನೂ ಸೂಚಿಸುತ್ತದೆ, ಇದರಲ್ಲಿ ಪ್ರಮಾಣವು ಅದರ ಮೂಲದ ಮಟ್ಟದಲ್ಲಿ ಅಥವಾ ಗ್ರಾಫ್ನ ಪ್ರಾರಂಭದಲ್ಲಿ ಕೊನೆಗೊಳ್ಳುತ್ತದೆ.
ಈ ಲೇಖನವು ಮುಖ್ಯ ಲಕ್ಷಣಗಳೊಂದಿಗೆ ಮುಕ್ತಾಯಗೊಳ್ಳುತ್ತದೆ ಎರಡೂ ಕಾರ್ಯಗಳು ಮತ್ತು ಅವುಗಳ ವ್ಯತ್ಯಾಸಗಳು. ಈ ಎರಡೂ ಕಾರ್ಯಗಳು ಗಣಿತ ಕ್ಷೇತ್ರದಲ್ಲಿ ಅಪಾರ ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು ಹೊಂದಿವೆ ಮತ್ತು ವಿಜ್ಞಾನ, ವಾಣಿಜ್ಯ ಮತ್ತು ನಮ್ಮ ದೈನಂದಿನ ಜೀವನದಲ್ಲಿಯೂ ಸಹ ವಿವಿಧ ಕ್ಷೇತ್ರಗಳಲ್ಲಿ ಅನ್ವಯಿಸಲ್ಪಡುತ್ತವೆ. ಆದ್ದರಿಂದ, ಈ ಎರಡು ಕಾರ್ಯಗಳ ಆಳವಾದ ತಿಳುವಳಿಕೆ ಮತ್ತು ಪಾಂಡಿತ್ಯವನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಲು ನಾನು ನಿಮ್ಮನ್ನು ಪ್ರೋತ್ಸಾಹಿಸುತ್ತೇನೆ.
ಆಶಾದಾಯಕವಾಗಿ, ಈ ಲೇಖನವನ್ನು ಓದಿದ ನಂತರ, ಈ ಎರಡನ್ನು ಹೇಗೆ ಪರಿಹರಿಸಲಾಗಿದೆ, ಅವುಗಳ ವ್ಯತ್ಯಾಸಗಳು, ಗ್ರಾಫ್ಗಳ ಬಗ್ಗೆ ನೀವು ಸ್ಪಷ್ಟವಾದ ತಿಳುವಳಿಕೆಯನ್ನು ಹೊಂದಿರಬಹುದು , ಮತ್ತು ಇನ್ನೂ ಬಹಳಷ್ಟು. ಗಣಿತಕ್ಕೆ ಸಂಬಂಧಿಸಿದ ಲೇಖನವು ನೀರಸವಾಗಿ ಕಾಣಿಸಬಹುದು ಆದರೆ ಇದನ್ನು ಓದಿದ ನಂತರ ನೀವು ಬಯಸುತ್ತೀರಿಸರಿಯಾದ ರೀತಿಯಲ್ಲಿ ತಲುಪಿಸಿದರೆ ಗಣಿತವೂ ಆಸಕ್ತಿಕರವಾಗಿರುತ್ತದೆ ಎಂಬುದನ್ನು ಅರಿತುಕೊಂಡಿದ್ದೇವೆ.

