দ্বিঘাত আৰু ঘাতীয় ফলনৰ মাজত পাৰ্থক্য কি? (পাৰ্থক্য ব্যাখ্যা কৰা হৈছে) – সকলো পাৰ্থক্য
বিষয়বস্তুৰ তালিকা
আপুনি হয়তো নৱম বা একাদশ শ্ৰেণীত আপোনাৰ পাঠ্যক্ৰমৰ অংশ হিচাপে দ্বিঘাত আৰু ঘাতীয় ফলন অধ্যয়ন কৰিছিল। কিন্তু এই কাৰ্য্যসমূহ আপোনাৰ পাঠ্যক্ৰমৰ অংশ হিচাপে অধ্যয়ন কৰিলে দুয়োটাৰ মাজৰ পাৰ্থক্যৰ বিষয়ে স্পষ্ট বুজাবুজি হ’বই লাগিব বুলি ক’ব নোৱাৰি।
আপোনাৰ পাঠ্যক্ৰমৰ অংশ হিচাপে, আপুনি দুয়োটাৰ মাজৰ সম্ভাৱ্য পাৰ্থক্য আৰু ইয়াৰ প্ৰয়োগৰ বিষয়ে কেতিয়াও অনুমান নকৰাকৈয়ে দুয়োটাৰ সৈতে জড়িত সমীকৰণ আৰু সমস্যাসমূহ সমাধান কৰিব লাগিব।
গতিকে এই লেখাটোত মই আপোনালোকক গ্ৰাফ, সমীকৰণ আৰু উদাহৰণৰ সহায়ত দুয়োটাৰ মাজৰ পাৰ্থক্যৰ বিষয়ে জ্ঞান দিয়াৰ লক্ষ্য ৰাখিছো যাতে আপুনি জ্ঞানটো সহজে বুজিব পাৰে।
আৰম্ভ কৰোঁ।
গণিতত ফাংচন কি?
গণিতত এটা ফাংচনক ইনপুটৰ মাজৰ সম্পৰ্ক হিচাপে সৰ্বোত্তমভাৱে সংজ্ঞায়িত কৰা হয় য'ত প্ৰতিটো ইনপুটৰ একে ফলাফল থাকে যাৰ অৰ্থ হ'ল প্ৰতিটো ইনপুটে একেটা আউটপুট ঘূৰাই দিব।
গণিতত এটা ফলন প্ৰায়ে f(x) দ্বাৰা দেখুওৱা হয় বা প্ৰতিনিধিত্ব কৰা হয়। উদাহৰণস্বৰূপে f(x)=x^2। এই ফাংচনে আমাক ব্ৰেকেটত থকা সংখ্যাটোৰ বৰ্গ দিব, এই ক্ষেত্ৰত, সংখ্যাটো ২।
ফাংচনটোত থকা ইনপুট যিয়েই নহওক কিয় ই আমাক একে আউটপুট দিব। এই ক্ষেত্ৰত ই সদায় ব্ৰেকেটত থকা সংখ্যাটোৰ বৰ্গটোক আউটপুট হিচাপে ঘূৰাই দিব।
গণিতত বহুতো ফাংচন আছে যিবোৰ বিভিন্ন কাম সম্পন্ন কৰিবলৈ ব্যৱহাৰ কৰা হয় আৰু সেইবোৰ বিভিন্ন ক্ষেত্ৰত প্ৰয়োগ কৰা হয়। অৱশ্যে আমি যিবোৰ ফাংচনৰ বিষয়ে আলোচনা কৰিবলৈ ওলাইছোএই প্ৰবন্ধটোত দ্বিঘাত আৰু ঘাতীয় ফলন দিয়া হৈছে। আমি মূলতঃ এই দুটা ফাংচনৰ মাজৰ পাৰ্থক্য উজ্জ্বল কৰাত গুৰুত্ব দিম।
দ্বিঘাত ফলন কি?
দ্বিঘাত ফলন এটা বহুপদ ফলন আৰু ই ax^2+bx+c সমীকৰণৰ যিকোনো ৰূপ। ইয়াক ডিগ্ৰী ২ ৰ বহুপদ বুলিও কোৱা হয় কাৰণ সৰ্বোচ্চ ঘাত ২ হ’ব পাৰে।
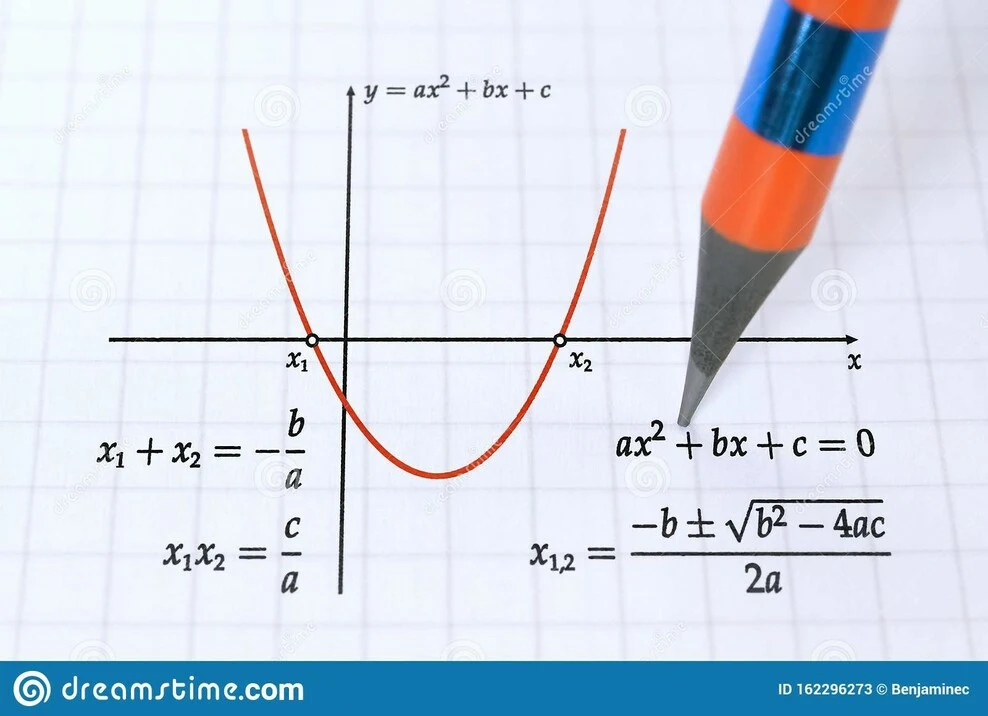
দ্বিঘাত সূত্ৰটো বিজ্ঞানৰ বিভিন্ন ক্ষেত্ৰত যেনে অভিযান্ত্ৰিক ক্ষেত্ৰত ব্যৱহাৰ কৰা হয়। ইয়াক পেৰাব’লাৰ জৰিয়তে চিত্ৰাংকিতভাৱে দেখুওৱা হৈছে।
এই পেৰাব’লাটো আমাৰ দৈনন্দিন জীৱনৰ বিভিন্ন কাম যেনে বল নিক্ষেপ কৰা বা গ’ল্ফ বল আঘাত কৰা আদিৰ বাবে ব্যৱহাৰ কৰা হয়। জোখত অনুপস্থিত চলক বিচাৰি উলিয়াবলৈ আৰু যিকোনো বস্তুৰ বেগ জানিবলৈ আৰু বাণিজ্যৰ ক্ষেত্ৰত যিকোনো বস্তু বা উৎপাদনৰ লাভ গণনা কৰিবলৈও দ্বিঘাত সমীকৰণ ব্যৱহাৰ কৰা হয়।
এটা দ্বিঘাত সমীকৰণৰ উদাহৰণ দিয়া হ'ল: 3x^ 2+5x+9 a:3 b:5 c:9
এইটো এটা দ্বিঘাত ফলনৰ এটা উদাহৰণ ইয়াৰ প্ৰামাণিক ৰূপত। এনে সমীকৰণ সমাধানৰ বাবে ব্যৱহাৰ কৰা সূত্ৰটোক দ্বিঘাত সূত্ৰ বুলি জনা যায়, যিটো হ’ল: (-b±√(b2-4ac))/(2a).
ঘাতীয় ফলন কি?
গণিতত এটা ঘাতীয় ফাংচন হৈছে এটা ফাংচন যিটো f(x)=a^x ৰূপত থাকে য'ত a হৈছে ভিত্তি, ই এটা ধ্ৰুৱক আৰু ই সদায় 0তকৈ ডাঙৰ হ'ব লাগিব f(x)=\exp বা e^{x} দ্বাৰা চিহ্নিত কৰা হয়।
সৰ্বাধিক ব্যৱহৃত ঘাতীয় ভিত্তি হৈছে ভিত্তি e যাক প্ৰাকৃতিক বুলি কোৱা হয়লগাৰিদম। ইয়াৰ সহায়ত জনসংখ্যা আৰু বেক্টেৰিয়া আদি বিভিন্ন বস্তুৰ বৃদ্ধিৰ হাৰ গণনা কৰা হয়। গণিতত এটা ঘাতীয় ফলন তৰ্কহীনভাৱে আটাইতকৈ গুৰুত্বপূৰ্ণ ফলন।
See_also: মংগোলীয় বনাম. হুন্স- (আপুনি জানিবলগীয়া সকলো) – All The Differencesই অতি গুৰুত্বপূৰ্ণ কাৰণ ইয়াক বিভিন্ন ক্ষেত্ৰত ব্যৱহাৰ কৰা হয় যেনে:
- বিজ্ঞান
- বাণিজ্য।
উদাহৰণস্বৰূপে, আপুনি বেংকত জমা কৰা ধনৰ সুতৰ হাৰ ঘাতীয়ভাৱে বৃদ্ধি পায় যাৰ অৰ্থ হৈছে ই এটা ঘাতীয় বক্ৰ অনুসৰণ কৰে গতিকে, ইয়াক ঘাতীয় ফলন ব্যৱহাৰ কৰি গণনা কৰিব পাৰি।
তদুপৰি, ঋণৰ বৃদ্ধিও ঘাতীয়ভাৱে বৃদ্ধি পায় আৰু এটা ঘাতীয় বক্ৰ অনুসৰণ কৰে, গতিকে, ঘাতীয় ফলন ব্যৱহাৰ কৰি আপুনি আপোনাৰ ঋণ বৃদ্ধিৰ পৰা ৰোধ কৰিব পাৰে আৰু আপোনাৰ বিত্তীয় ক্ষেত্ৰত অধিক নিয়ন্ত্ৰণ ৰাখিব পাৰে।
See_also: ৯.৫ বনাম ১০ জোতাৰ আকাৰ: আপুনি কেনেকৈ পাৰ্থক্য কৰিব পাৰে? – অল দ্য ডিফাৰেন্সজীৱবিজ্ঞানত ইয়াক এটা নিৰ্দিষ্ট সময়ৰ ভিতৰত এটা নিৰ্দিষ্ট অঞ্চলৰ জনসংখ্যা বৃদ্ধিৰ অনুমান কৰিবলৈ ব্যৱহাৰ কৰা হয়।
ইউৰেনিয়ামৰ ক্ষয়ৰ দৰে ৰেডিঅ’ক্ৰিয়াশীলতাইও ঘাতীয় বৃদ্ধিৰ পিছত লয়। এইদৰে এইটো ঘাতীয় ফলনৰ আন এটা প্ৰয়োগ।
পদাৰ্থ বিজ্ঞানত sin, cos, শব্দ তৰংগ, আৰু আন বহুতো তৰংগ আদি সকলো তৰংগকে ঘাতীয় ফলনৰ ক্ষেত্ৰতো লিখিব পাৰি গতিকে এই ফলনে পদাৰ্থবিজ্ঞানীসকলক এই তৰংগসমূহৰ ওপৰত গৱেষণা কৰাত সহায় কৰে।
কি দ্বিঘাত গ্ৰাফ নেকি?

এইটো এটা দ্বিঘাত গ্ৰাফৰ প্ৰতিনিধিত্ব
দ্বিঘাত ফলনৰ গ্ৰাফটো ওপৰৰ ছবিখনত দেখুওৱাৰ দৰে এটা U আকৃতিৰ পেৰাব’লা। এই পেৰাব’লাটো হয় হাঁহিৰ দৰে খোল খাব পাৰে নহয় ভ্ৰু কোঁচাই লোৱাৰ দৰে তললৈ খোল খাব পাৰে। দ্য...পেৰাব’লাটো মুকলি হোৱাৰ ধৰণটো সহগটোৰ ওপৰত নিৰ্ভৰ কৰে: ax^2+bx+c সমীকৰণটোত ”a”। যদি সহগটো a>0 হয় তেন্তে পেৰাব’লাটো খোল খায় আৰু যদি সহগটো a<0 হয় তেন্তে পেৰাব’লাটো তললৈ খোল খায়।
- পেৰাব’লাৰ সৰ্বোচ্চ বা নিম্নতম বিন্দুটোক শিখৰ বোলা হয়।
- শিখৰে প্ৰতিনিধিত্ব কৰা বিন্দুটো, সৰ্বোচ্চ বা সৰ্বনিম্ন হওক, ই পেৰাব'লাটো খোলাৰ ধৰণৰ ওপৰত নিৰ্ভৰ কৰে।
যদি ই খোল খায় তেন্তে শিখৰে গ্ৰাফৰ নূন্যতম বিন্দুটোক প্ৰতিনিধিত্ব কৰে আৰু যদি ই তাৰ পিছত শিখৰে দ্বিঘাত গ্ৰাফত সৰ্বোচ্চ বিন্দুটোক প্ৰতিনিধিত্ব কৰে। পেৰাব'লাৰ আন এটা বৈশিষ্ট্য হ'ল প্ৰতিসমতা ৰেখা যিটো হৈছে শিখৰৰ মাজেৰে পাৰ হৈ যোৱা এটা উলম্ব ৰেখা আৰু ইয়াক পেৰাব'লাক ২টা সমান আৰু একে অৰ্ধেকত বিভক্ত কৰিবলৈ ব্যৱহাৰ কৰা হয়।
তল সূত্ৰটো ব্যৱহাৰ কৰি ইয়াক লাভ কৰিব পাৰি: y =a(x−h)2+k। দ্বিঘাত গ্ৰাফত এটা y-অন্তৰ্চ্ছেদ থাকে যিটো হৈছে সেই বিন্দু য’ত পেৰাব’লাটোৱে y-অক্ষক ছেদ কৰে। এই y-intercept ৰ মাত্ৰ এটা মান আছে অৰ্থাৎ পেৰাব’লাটোৱে y অক্ষক এবাৰহে ছেদ কৰে। x-অন্তৰ্চ্ছেদ হৈছে সেই বিন্দু য'ত পেৰাব'লাই x-অক্ষক বাধা দিয়ে বা অতিক্ৰম কৰে।
অন্তৰ্চ্ছেদৰ সংখ্যা 0, 1, বা 2 হ'ব পাৰে ২টালৈকে দ্ৰৱ বা ২টা শিপা থাকে। দ্বিঘাত গ্ৰাফ হৈছে দ্বিঘাত সমীকৰণ সমাধানৰ এটা উপায়। ইয়াক দ্বিঘাত সমীকৰণ সমাধানৰ চিত্ৰাংকিত পদ্ধতি বুলি কোৱা হয়।
দ্বিঘাত গ্ৰাফ ব্যৱহাৰ কৰা হয়আমাৰ দৈনন্দিন জীৱনৰ বহু ক্ষেত্ৰত মূলতঃ ক্ৰীড়াৰ ক্ষেত্ৰত। বল নিক্ষেপ কৰা বা উচ্চ মঞ্চৰ পৰা জপিয়াই পৰা, এনে পৰিস্থিতিৰ উদাহৰণ যিবোৰ দ্বিঘাত গ্ৰাফৰ দ্বাৰা প্ৰদৰ্শন কৰিব পৰা যাব। তাৰ পিছত দ্বিঘাত গ্ৰাফ ব্যৱহাৰ কৰি বল বা ব্যক্তিজনে পোৱা সৰ্বোচ্চ বা নূন্যতম বিন্দু বিচাৰি উলিয়াব পাৰি।
ঘাতীয় গ্ৰাফ কি?
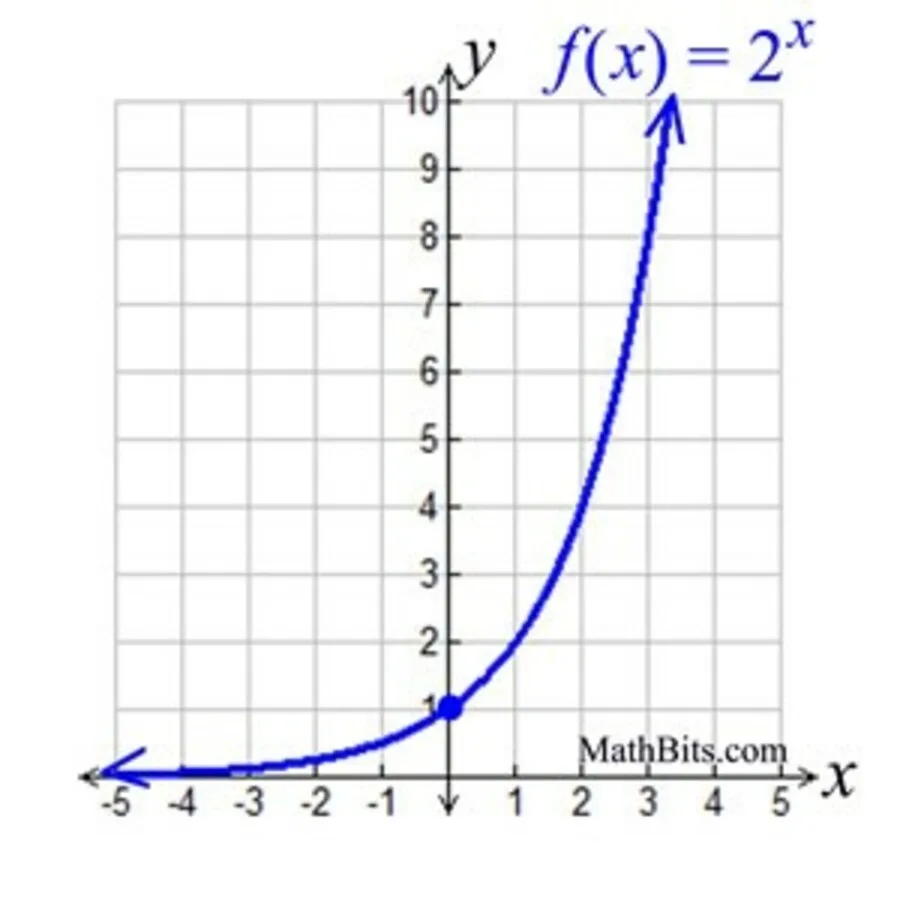
এইটো এটা ঘাতীয় গ্ৰাফৰ প্ৰতিনিধিত্ব
বীজগণিতীয় আৰু অতিক্ৰমণীয় সমীকৰণ দুয়োটাকে প্ৰায়ে কেলকুলেটৰৰ সহায়ত হাতেৰে সমাধান কৰিব পাৰি, কিন্তু যেতিয়া এই দুটা সমীকৰণ, বীজগণিতীয় আৰু... অতিক্ৰমণীয় একেলগে দেখা দিয়ে, হাতেৰে সমাধান কৰাটো অতি কঠিন বা আনকি অসম্ভৱ হৈ পৰে। গতিকে এই দুটা সমীকৰণ একেলগে সমাধান কৰিবলৈ আমি ঘাতীয় গ্ৰাফটো ব্যৱহাৰ কৰি ইয়াক চিত্ৰাংকিতভাৱে সমাধান কৰোঁ।
সৰলতম ঘাতীয় ফলনটো হ’ল f(x) = ax, a>0, a≠1। এই ফাংচনত, ভিত্তি a সদায় 0 তকৈ ডাঙৰ ৰখা হয় কাৰণ যদি ভিত্তি 0 তকৈ কম হয় তেন্তে ই আমাক এটা অবাস্তৱ সংখ্যা দিব পাৰে।
যদি ভিত্তিটো 1 হয় তেন্তে ইয়াৰ ঘাত নিৰ্বিশেষে ই সদায় 1 ঘূৰাই দিব আৰু ই এটা অতি বিৰক্তিকৰ ফলন হ'ব। এই কাৰণসমূহৰ বাবেই ঘাতীয় ফলনটোৰ ওপৰত কিছুমান নিষেধাজ্ঞা আৰোপ কৰা হয়।
ঘাতীয় ফলনৰ গ্ৰাফে ভিত্তিটো ১তকৈ ডাঙৰ বা ১তকৈ কম কিন্তু ০তকৈ বেছি তাৰ ওপৰত নিৰ্ভৰ কৰি বিভিন্ন বৈশিষ্ট্য প্ৰদৰ্শন কৰে নিম্নলিখিত বৈশিষ্ট্যসমূহ প্ৰদৰ্শন কৰক যেতিয়া ভিত্তিই কৰিবডমেইনটো কেৱল বাস্তৱ সংখ্যাৰে গঠিত হ'ব, পৰিসীমা হ'ব y>0, গ্ৰাফটো অহৰহ বৃদ্ধি পাব, গ্ৰাফটো অবিৰত হ'ব আৰু ই মসৃণ হ'ব।
ঘাতীয় গ্ৰাফটোৱে একেধৰণৰ দেখুৱাইছে ভিত্তি 1 তকৈ কম কিন্তু 0 তকৈ ডাঙৰ হ'লে বৈশিষ্ট্যসমূহ। ইয়াৰ বৈশিষ্ট্যসমূহৰ একমাত্ৰ পৰিৱৰ্তন হ'ল যে গ্ৰাফটো হ্ৰাস পাব। ঘাতীয় ফলনৰ জৰিয়তে পোৱা তথ্যক প্ৰতিনিধিত্ব কৰিবলৈ ঘাতীয় গ্ৰাফ ব্যৱহাৰ কৰা হয়। তথ্যৰ প্ৰকাৰ আৰু ঘাতীয় ফলনৰ প্ৰয়োগৰ বিষয়ে পূৰ্বে আলোচনা কৰা হৈছে।
ঘাতীয় আৰু দ্বিঘাত ফলনৰ মাজৰ পাৰ্থক্য (ইয়াত বিষয়বস্তুক টেবুল হিচাপে ব্যৱহাৰ কৰক)
এতিয়া যেতিয়া দ্বিঘাত আৰু... ঘাতীয় ফলন বিকশিত কৰা হৈছে আমি এই দুটা অতি গুৰুত্বপূৰ্ণ ফলনৰ মাজৰ পাৰ্থক্যৰ বিষয়ে আলোচনা কৰিম।
| দ্বিঘাত ফলন | ঘাতীয় ফলন |
|---|---|
| চলকটো হৈছে ভিত্তি আৰু সৰ্বোচ্চ সম্ভাৱ্য শক্তি হ'ল (ax^2+bx+c)। | ভিত্তিটো এটা ধ্ৰুৱক আৰু সেই ভিত্তিৰ শক্তি এটা চলক। |
| পৰিৱৰ্তনৰ হাৰ ধ্ৰুৱক যাৰ অৰ্থ হ'ল গ্ৰাফটো স্থিৰ হাৰত বৃদ্ধি পায় আৰু সেয়েহে এটা নিৰ্দিষ্ট সময়ৰ ভিতৰত গ্ৰাফটোৰ পৰিৱৰ্তন গণনা কৰাটো সহজ। | এটা... ঘাতীয় ফলন, পৰিৱৰ্তনৰ হাৰ নিজৰ সমানুপাতিক হয়, আৰু গ্ৰাফটো বৃদ্ধি পোৱা হাৰত বৃদ্ধি পায়। |
| দ্বিঘাত গ্ৰাফটোৱে a গঠন কৰিবপেৰাব'লা যেতিয়া ই ওপৰলৈ বা তললৈ দিশত শিখৰত উপনীত হয়। | এটা ঘাতীয় গ্ৰাফ এটা দিশত ওপৰলৈ বা তললৈ পৰি থাকিব। |
| এটা দ্বিঘাত গ্ৰাফ বক্ৰ যেতিয়া ই ইয়াৰ সৰ্বোচ্চ বা সৰ্বনিম্ন বিন্দুত উপনীত হয়। | এটা ঘাতীয় গ্ৰাফ আৰম্ভণিৰে পৰাই বক্ৰ হৈ থাকে। |
দ্বিঘাত ফলন বনাম ঘাতীয় ফলন
উপসংহাৰ
দুয়োটাৰ মাজৰ পাৰ্থক্য সম্পূৰ্ণৰূপে বুজিবলৈ এটা চমু ব্যাখ্যা
সামগ্ৰিকভাৱে ক'বলৈ গ'লে, দ্বিঘাত ফলন আৰু ঘাতীয় ফলনসমূহৰ প্ৰয়োগ আৰু ধাৰণাত ইটোৱে সিটোৰ পৰা পৃথক। ঘাতীয় ফলনে নিৰন্তৰ বৃদ্ধিৰ ইংগিত দিয়ে আনহাতে দ্বিঘাত ফলনে বৃদ্ধি আৰু হ্ৰাস দুয়োটাকে সূচায় য'ত পৰিমাণটো ইয়াৰ উৎপত্তিস্থল বা গ্ৰাফৰ আৰম্ভণিৰ স্তৰত শেষ হয়।
এই প্ৰবন্ধটোৰ সামৰণি পৰে দুয়োটা কাৰ্য্যৰ লগতে ইহঁতৰ পাৰ্থক্যও। এই দুয়োটা কাৰ্য্যই গণিতৰ ক্ষেত্ৰত অপৰিসীম গুৰুত্বপূৰ্ণ আৰু ইয়াক বিজ্ঞান, বাণিজ্য, আৰু আমাৰ দৈনন্দিন জীৱনৰ দৰে বিভিন্ন ক্ষেত্ৰতো প্ৰয়োগ কৰা হয়। গতিকে মই আপোনালোকক এই দুটা কাৰ্য্যৰ ওপৰত গভীৰ বুজাবুজি আৰু আয়ত্ত গঢ়ি তুলিবলৈ উৎসাহিত কৰিম।
আশাকৰোঁ এই লেখাটো পঢ়াৰ পিছত এই দুটা কেনেকৈ সমাধান কৰা হয়, ইয়াৰ পাৰ্থক্য, গ্ৰাফৰ বিষয়ে স্পষ্ট বুজাবুজি হ'ব পাৰে , আৰু বহুত কিবাকিবি। গণিতৰ লগত জড়িত এটা লেখা বিৰক্তিকৰ যেন লাগিব পাৰে কিন্তু এইটো পঢ়াৰ পিছত আপুনি কৰিবউপলব্ধি কৰিছে যে আনকি গণিতকো সঠিকভাৱে প্ৰদান কৰিলে আকৰ্ষণীয় হ'ব পাৰে।

