Quadratic နှင့် Exponential Function အကြား ကွာခြားချက်ကား အဘယ်နည်း။ (ကွဲပြားမှုကို ရှင်းပြသည်) - ကွဲပြားမှုအားလုံး
မာတိကာ
သင် 9th သို့မဟုတ် 11th တန်းတွင် သင့် syllabus ၏ တစ်စိတ်တစ်ပိုင်းအနေဖြင့် Quadratic နှင့် Exponential လုပ်ဆောင်ချက်များကို လေ့လာဖူးပေမည်။ သို့သော်၊ သင်၏ သင်ရိုးညွှန်းတမ်း၏ တစ်စိတ်တစ်ပိုင်းအနေဖြင့် ဤလုပ်ဆောင်ချက်များကို လေ့လာခြင်းသည် ၎င်းတို့နှစ်ခုကြား ခြားနားချက်ကို ရှင်းရှင်းလင်းလင်း နားလည်ရန် မလိုအပ်ပါ။
သင်ရိုးမာတိကာ၏တစ်စိတ်တစ်ပိုင်းအနေဖြင့်၊ ၎င်းတို့နှစ်ခုနှင့် ၎င်းတို့၏အသုံးချပလီကေးရှင်းနှစ်ခုကြား ဖြစ်နိုင်ချေရှိသော ကွာခြားချက်များကို မည်သည့်အခါမျှ မတွေးတောဘဲ ညီမျှခြင်းများနှင့် ပြဿနာများကို သင်ဖြေရှင်းရန်သာ လိုအပ်ပါသည်။
ထို့ကြောင့် ဤဆောင်းပါးတွင်၊ ဂရပ်များ၊ ညီမျှခြင်းများနှင့် ဥပမာများအကူအညီဖြင့် အသိပညာကို လွယ်ကူစွာနားလည်နိုင်စေရန် ရည်ရွယ်ပါသည်။
ကြည့်ပါ။: အလုပ်ထုတ်ခံရခြင်း VS လွှတ်လိုက်ခြင်း- ကွာခြားချက်ကား အဘယ်နည်း။ - ကွဲပြားမှုအားလုံးစကြရအောင်။
သင်္ချာမှာ Function ဆိုတာဘာလဲ။
သင်္ချာရှိ လုပ်ဆောင်ချက်တစ်ခုသည် input တစ်ခုစီတွင် တူညီသောရလဒ်ရှိသည့်အတွက် input တစ်ခုစီသည် တူညီသော output ကိုပြန်ပေးမည့် inputs များကြားဆက်စပ်မှုအဖြစ် အကောင်းဆုံးသတ်မှတ်ထားသည်။
သင်္ချာတွင် ဖန်ရှင်တစ်ခုကို f(x) ဖြင့် သို့မဟုတ် ကိုယ်စားပြုလေ့ရှိသည်။ ဥပမာ f(x)=x^2။ ဤလုပ်ဆောင်ချက်သည် ကွင်းကွင်းအတွင်းရှိ နံပါတ်၏ နှစ်ထပ်ကို ပေးမည်ဖြစ်ပြီး၊ ဤကိစ္စတွင်၊ နံပါတ် 2 ဖြစ်သည်။
၎င်းသည် ကျွန်ုပ်တို့အား လုပ်ဆောင်ချက်တွင် ထည့်သွင်းမှုမည်မျှပင်ရှိစေကာမူ တူညီသောအထွက်ကို ပေးမည်ဖြစ်သည်။ ဤကိစ္စတွင်၊ ၎င်းသည် အထွက်အဖြစ် ကွင်းစကွင်းလယ်ရှိ ဂဏန်း၏ နှစ်ထပ်ကိန်းကို အမြဲတမ်း ပြန်ပေးပါမည်။
မတူညီသော အလုပ်များကို ပြီးမြောက်ရန်အတွက် အသုံးပြုသည့် သင်္ချာတွင် လုပ်ဆောင်ချက်များစွာရှိပြီး ၎င်းတို့ကို နယ်ပယ်အမျိုးမျိုးတွင် အသုံးချပါသည်။ ဒါပေမယ့် ကျွန်တော်တို့ ဆွေးနွေးရမယ့် လုပ်ငန်းဆောင်တာတွေ ရှိတယ်။ဤဆောင်းပါးတွင် လေးထောင့်ကိန်းနှင့် ထပ်ကိန်းလုပ်ဆောင်ချက်များဖြစ်သည်။ ဤလုပ်ဆောင်ချက်နှစ်ခုကြား ခြားနားချက်ကို မီးမောင်းထိုးပြရန် ကျွန်ုပ်တို့ အဓိကအာရုံစိုက်ပါမည်။
လေးပုံတစ်ပုံလုပ်ဆောင်မှုဟူသည် အဘယ်နည်း။
လေးထောင့်ကိန်း လုပ်ဆောင်ချက်သည် ပေါင်းကူးအမည် လုပ်ဆောင်ချက်ဖြစ်ပြီး ၎င်းသည် ညီမျှခြင်း ax^2+bx+c ၏ မည်သည့်ပုံစံဖြစ်သည်။ အမြင့်ဆုံး ထပ်ကိန်းသည် 2 ဖြစ်သည့်အတွက်ကြောင့် ဒီဂရီ 2 ၏ ပေါလီအမည်ဟုလည်း ခေါ်သည်။
လေးထောင့်ပုံသေနည်းကို အင်ဂျင်နီယာ ကဲ့သို့သော သိပ္ပံနယ်ပယ်အမျိုးမျိုးတွင် အသုံးပြုသည်။ ၎င်းကို parabola မှတဆင့် ဂရပ်ဖစ်ဖြင့် ကိုယ်စားပြုပါသည်။
ဤ parabola ကို ဘောလုံးပစ်ခြင်း သို့မဟုတ် ဂေါက်သီးရိုက်ခြင်းကဲ့သို့သော ကျွန်ုပ်တို့၏နေ့စဉ်ဘဝများတွင် မတူညီသောလှုပ်ရှားမှုများအတွက် အသုံးပြုပါသည်။ Quadratic equation များကို တိုင်းတာခြင်းများတွင် ပျောက်ဆုံးနေသော ကိန်းရှင်များကို ရှာဖွေရန်နှင့် မည်သည့်အရာဝတ္ထု၏ အလျင်ကို ရှာဖွေရန်နှင့် ကူးသန်းရောင်းဝယ်ရေးနယ်ပယ်တွင် မည်သည့်ပစ္စည်း သို့မဟုတ် ထုတ်ကုန်များ၏ အမြတ်ငွေကို တွက်ချက်ရန်အတွက်လည်း အသုံးပြုပါသည်။
ဤသည်မှာ လေးထောင့်ညီမျှခြင်း၏ ဥပမာတစ်ခုဖြစ်သည်- 3x^ 2+5x+9 a:3 b:5 c:9
၎င်းသည် ၎င်း၏စံပုံစံရှိ လေးထောင့်ပုံစံလုပ်ဆောင်ချက်၏ ဥပမာတစ်ခုဖြစ်သည်။ ထိုညီမျှခြင်းများကို ဖြေရှင်းရန် အသုံးပြုသည့် ဖော်မြူလာကို အောက်ဖော်ပြပါအရာဖြစ်သည့် လေးထောင့်ပုံသေနည်းဟု လူသိများသည်- (-b±√(b²-4ac))/(2a)။
အညွှန်းကိန်း လုပ်ဆောင်ချက်ဆိုသည်မှာ အဘယ်နည်း။
သင်္ချာရှိ အညွှန်းကိန်းတစ်ခုသည် f(x)=a^x ဟူသော ပုံစံဖြင့် a သည် အခြေခံဖြစ်ပြီး၊ ၎င်းသည် ကိန်းသေတစ်ခုဖြစ်ပြီး ၎င်းသည် 0 ထက် အမြဲကြီးနေရမည်ဖြစ်သည်။ f(x)=\exp သို့မဟုတ် e^{x} ဖြင့် ရည်ညွှန်းသည်။
အသုံးအများဆုံး ကိန်းဂဏန်းမှာ သဘာဝ e ဟုခေါ်သော အခြေခံ e ဖြစ်သည်။လော့ဂရစ်သမ် လူဦးရေနှင့် ဘက်တီးရီးယားကဲ့သို့သော အရာအမျိုးမျိုး၏ ကြီးထွားနှုန်းကို တွက်ချက်ရန် ၎င်းကို အသုံးပြုသည်။ exponential function သည် သင်္ချာတွင် အရေးကြီးဆုံး function ဖြစ်သည်ဟု ယူဆပါသည်။
၎င်းကို အောက်ပါကဲ့သို့သော နယ်ပယ်အသီးသီးတွင် အသုံးပြုသောကြောင့် ၎င်းကို အလွန်အရေးကြီးပါသည်။
ဥပမာ၊ ဘဏ်တစ်ခုတွင် သင်အပ်ငွေအပေါ် အတိုးနှုန်းသည် အဆတိုးလာသဖြင့် ၎င်းသည် အတိုးကိန်းမျဉ်းကွေးတစ်ခုသို့ လိုက်နေသောကြောင့် ၎င်းကို အတိုးကိန်းလုပ်ဆောင်ချက်များကို အသုံးပြု၍ တွက်ချက်နိုင်သည်။
ထို့ပြင်၊ ကြွေးမြီကြီးထွားမှုသည် အဆတိုးပြီး အဆကိန်းဂုတ်ကို လိုက်နာသောကြောင့်၊ ကိန်းဂဏန်းလုပ်ဆောင်ချက်များကို အသုံးပြုခြင်းဖြင့် သင့်အကြွေးများတက်လာခြင်းမှ ရပ်တန့်နိုင်ပြီး သင့်ဘဏ္ဍာရေးအပေါ် ပိုမိုထိန်းချုပ်နိုင်မည်ဖြစ်သည်။
ဇီဝဗေဒတွင်၊ သတ်မှတ်ထားသော ဧရိယာတစ်ခုအတွင်း လူဦးရေတိုးလာမှုကို ခန့်မှန်းရန် ၎င်းကို အသုံးပြုသည်။
ယူရေနီယံ၏ ယိုယွင်းပျက်စီးခြင်းကဲ့သို့သော ရေဒီယိုသတ္တိကြွမှုမှာလည်း ထပ်ကိန်းတိုးနှုန်းနောက်ဆက်တွဲဖြစ်သည်။ ထို့ကြောင့်၊ ဤသည် exponential function ၏နောက်ထပ် application တစ်ခုဖြစ်သည်။
ရူပဗေဒတွင် sin၊ cos၊ sound waves နှင့် အခြားသော waves များအားလုံးကို exponential functions များအဖြစ် ရေးသားနိုင်သောကြောင့် ဤ function သည် ရူပဗေဒပညာရှင်များအား ဤလှိုင်းများကို ရှာဖွေရာတွင် အထောက်အကူဖြစ်စေပါသည်။
ဘာလဲ၊ Quadratic Graph တစ်ခုလား။

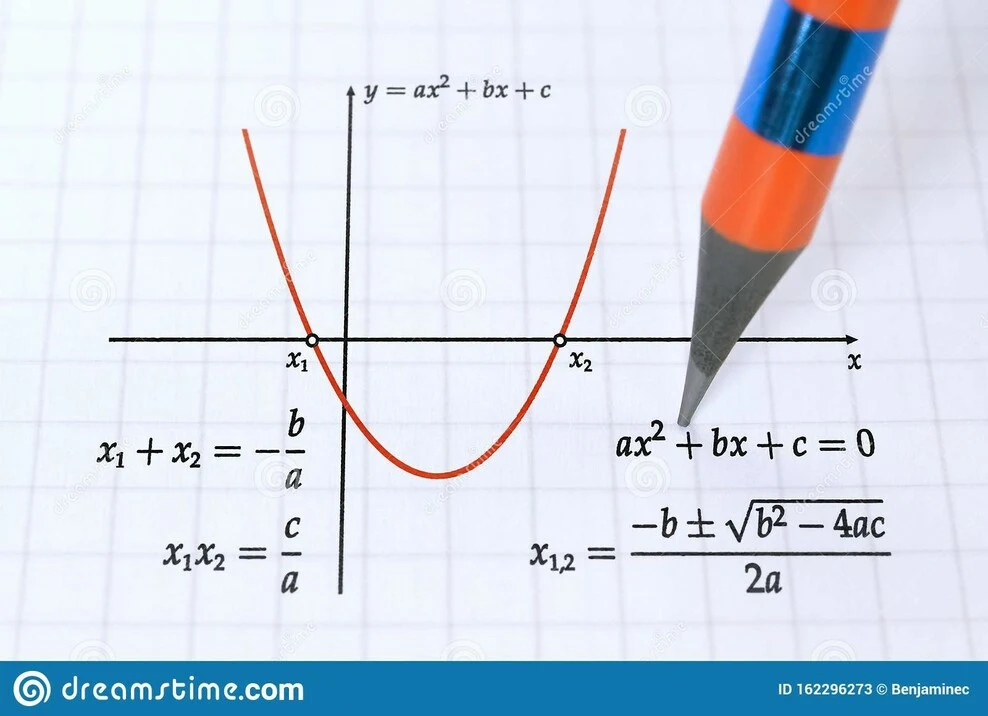
၎င်းသည် လေးထောင့်ပုံဂရပ်ကို ကိုယ်စားပြုခြင်းဖြစ်သည်
စတုရန်းပုံ လုပ်ဆောင်ချက်၏ ဂရပ်သည် အထက်ပုံတွင် ပြထားသည့်အတိုင်း U-shaped parabola ဖြစ်သည်။ ဤ parabola သည် အပြုံးကဲ့သို့ ဖွင့်နိုင်သည် သို့မဟုတ် မျက်မှောင်ကြုတ်သကဲ့သို့ အောက်ဘက်သို့ ဖွင့်နိုင်သည်။ ဟိပါရာဘိုလာဖွင့်နည်းသည် ညီမျှခြင်း ax^2+bx+c ရှိ ကိန်းကိန်းပေါ်တွင် မူတည်သည်။ coefficient သည် a>0 ဆိုလျှင် parabola ပွင့်လာပြီး coefficient သည် a<0 ဆိုလျှင် parabola ပွင့်သွားပါသည်။
- ပါရာဘိုလာ၏ အမြင့်ဆုံး သို့မဟုတ် အနိမ့်ဆုံးအမှတ်ကို vertex ဟုခေါ်သည်။
- ထိပ်တန်းကို ကိုယ်စားပြုသည့်အချက်သည် အမြင့်ဆုံး သို့မဟုတ် အနိမ့်ဆုံးဖြစ်မဖြစ် ပါရာဘိုလာပွင့်သည့်ပုံစံပေါ်တွင် မူတည်သည်။
၎င်းသည် အပေါ်သို့ပွင့်လာပါက၊ ဒေါင်လိုက်သည် ဂရပ်ပေါ်ရှိ အနိမ့်ဆုံးအမှတ်ကို ကိုယ်စားပြုပြီး ၎င်းသည် ရှိပါက၊ ပွင့်သွားပြီးနောက် vertex သည် လေးထောင့်ပုံဂရပ်ရှိ အမြင့်ဆုံးအမှတ်ကို ကိုယ်စားပြုသည်။ ပါရာဘိုလာ၏နောက်ထပ်အင်္ဂါရပ်မှာ ဒေါင်လိုက်မျဉ်းကိုဖြတ်သွားသည့် ဒေါင်လိုက်မျဉ်းကြောင်းဖြစ်သည့် အချိုးညီမျဉ်းကြောင်းနှင့် ပါရာဘိုလာကို အညီအမျှနှင့် ထပ်တူနှစ်ခြမ်းခွဲရန် အသုံးပြုသည်။
၎င်းကို အောက်ပါဖော်မြူလာကို အသုံးပြု၍ ရရှိနိုင်သည်- y =a(x−h)2+k။ လေးထောင့်ပုံဂရပ်တွင် ပါရာဘိုလာသည် y ဝင်ရိုးကိုဖြတ်သည့်နေရာဖြစ်သည့် y-ကြားဖြတ်တစ်ခုရှိသည်။ ဤ y-ကြားဖြတ်သည် ပါရာဘိုလာသည် y ဝင်ရိုးကို တစ်ကြိမ်သာ ဖြတ်တောက်သည်ဟု အဓိပ္ပာယ်ရသော တန်ဖိုးတစ်ခုသာ ရှိသည်။ x-ကြားဖြတ်သည် ပါရာဘိုလာကြားဖြတ် သို့မဟုတ် x-ဝင်ရိုးကိုဖြတ်သွားသည့်အမှတ်ဖြစ်သည်။
ကြားဖြတ်အရေအတွက်သည် 0၊ 1 သို့မဟုတ် 2 ဖြစ်နိုင်ပါသည်။ လေးထောင့်ကိန်းညီမျှခြင်းတစ်ခုသာလုပ်ဆောင်နိုင်သောကြောင့် ကြားဖြတ်အရေအတွက်အများဆုံးမှာ 2 ဖြစ်သည်။ ဖြေရှင်းချက် 2 ခု သို့မဟုတ် အမြစ် 2 ခုအထိရှိသည်။ လေးထောင့်ပုံဂရပ်သည် လေးထောင့်ညီမျှခြင်းများကို ဖြေရှင်းရန် နည်းလမ်းတစ်ခုဖြစ်သည်။ ၎င်းကို လေးထောင့်ကိန်းညီမျှခြင်းများကို ဖြေရှင်းသည့် ဂရပ်ဖစ်နည်းဟု ခေါ်သည်။
လေးထောင့်ပုံဂရပ်ကို အသုံးပြုသည်။ကျွန်ုပ်တို့၏နေ့စဉ်ဘဝ၏ နယ်ပယ်များစွာတွင် အဓိကအားဖြင့် အားကစားဖြစ်သည်။ ဘောလုံးကို ပစ်ခြင်း သို့မဟုတ် မြင့်မားသောပလက်ဖောင်းမှ ခုန်ခြင်းများသည် လေးထောင့်ပုံဂရပ်ဖြင့် သရုပ်ပြနိုင်သည့် အခြေအနေများ ဥပမာများဖြစ်သည်။ ထို့နောက် ဘောလုံး သို့မဟုတ် လူရောက်ရှိနေသည့် အများဆုံး သို့မဟုတ် အနိမ့်ဆုံး အမှတ်များကို ရှာဖွေရန် လေးထောင့်ပုံဂရပ်ကို အသုံးပြုနိုင်သည်။
အညွှန်းကိန်းဂရပ်များသည် အဘယ်နည်း။
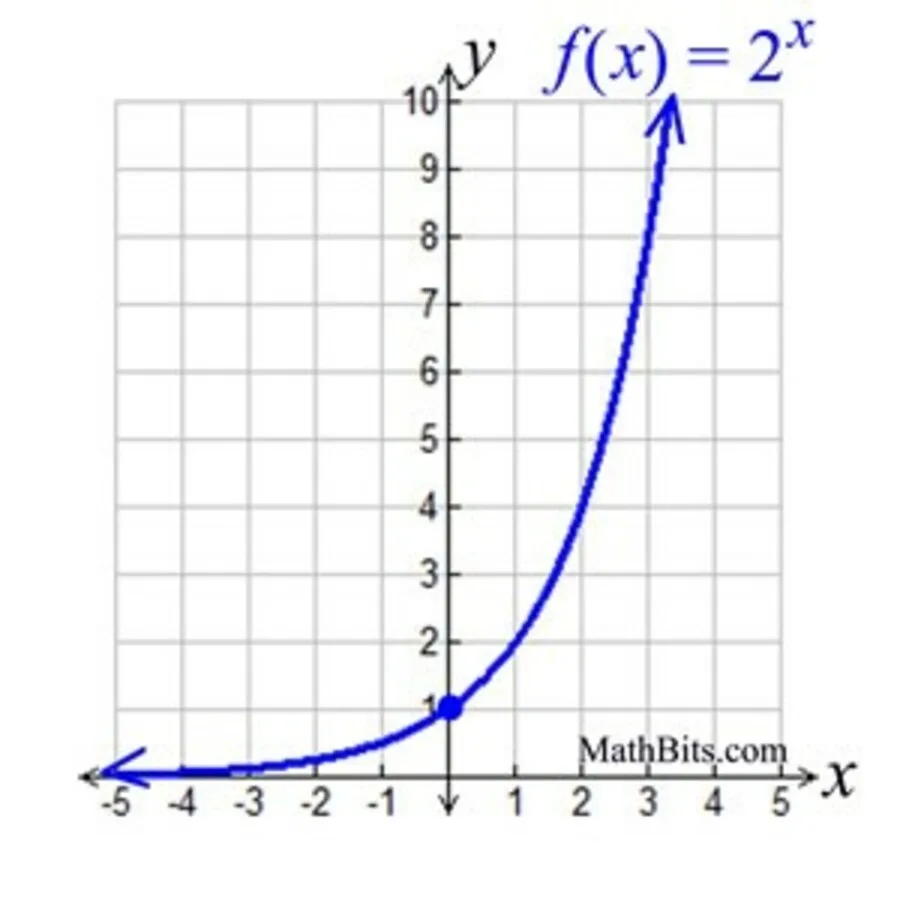
၎င်းသည် အညွှန်းကိန်းဂရပ်တစ်ခု၏ ကိုယ်စားပြုမှုတစ်ခုဖြစ်သည်
အက္ခရာသင်္ချာနှင့် အဘိညာဉ်ဆိုင်ရာညီမျှခြင်းနှစ်ခုလုံးကို ဂဏန်းပေါင်းစက်၏အကူအညီဖြင့် မကြာခဏဆိုသလို လက်ဖြင့်ဖြေရှင်းနိုင်သော်လည်း၊ ဤညီမျှခြင်းနှစ်ခု၊ အက္ခရာသင်္ချာနှင့်၊ အဘိညာဉ်တွေ တညီတညွတ်တည်း ပေါ်လာတော့ လက်နဲ့ဖြေရှင်းရတာ အရမ်းခက်တယ် ဒါမှမဟုတ် မဖြစ်နိုင်တာတွေတောင် ဖြစ်လာတယ်။ ထို့ကြောင့် ဤညီမျှခြင်းနှစ်ခုကို အတူတကွဖြေရှင်းရန်အတွက်၊ ကျွန်ုပ်တို့သည် အထပ်ကိန်းဂရပ်ကိုအသုံးပြုပြီး ဂရပ်ဖစ်ဖြင့်ဖြေရှင်းပါသည်။
ကြည့်ပါ။: အရေအတွက်အားလုံး Vs. မျက်နှာစာအားလုံး (ကွဲပြားမှုများ) - အားလုံးသော ကွဲပြားမှုများအရိုးရှင်းဆုံးကိန်းဂဏန်းလုပ်ဆောင်ချက်မှာ f(x) = ax, a>0, a≠1။ ဤ function တွင် base a သည် 0 ထက် ကြီးနေမည်ဖြစ်သောကြောင့် base သည် 0 ထက်နည်းပါက၊ ၎င်းသည် ကျွန်ုပ်တို့အား အစစ်အမှန်ကိန်းဂဏာန်းများကို ပေးနိုင်ပါသည်။
အခြေခံသည် 1 ဖြစ်ပါက ၎င်းသည် ၎င်း၏ ထပ်ကိန်းမခွဲခြားဘဲ 1 အမြဲပြန်နေမည်ဖြစ်ပြီး ၎င်းသည် အလွန်ငြီးငွေ့ဖွယ်ကောင်းသော လုပ်ဆောင်မှုတစ်ခုဖြစ်လာမည်ဖြစ်သည်။ ဤအကြောင်းများကြောင့် ကန့်သတ်ချက်အချို့ကို အညွှန်းကိန်းလုပ်ဆောင်မှုတွင် ထားရှိခြင်းဖြစ်သည်။
ကိန်းဂဏန်းတစ်ခု၏ ဂရပ်သည် 1 ထက် ကြီးသည် သို့မဟုတ် 1 ထက်နည်းသော်လည်း 0 ထက် ကြီးသည်ဖြစ်စေ အပေါ်မူတည်၍ မတူညီသော ဂုဏ်သတ္တိများကို ပြသပေးမည်ဖြစ်သည်။ အခြေတည်သောအခါတွင် အောက်ပါဂုဏ်သတ္တိများကို ပြသပါ။1 ထက် ပိုကြီးသည်။ ဒိုမိန်းတွင် ကိန်းဂဏာန်းအစစ်အမှန်များသာ ပါဝင်မည်ဖြစ်ပြီး အပိုင်းအခြားသည် y>0 ဖြစ်လိမ့်မည်၊ ဂရပ်သည် အဆက်မပြတ်တိုးလာမည်၊ ဂရပ်သည် စဉ်ဆက်မပြတ်ဖြစ်နေမည်ဖြစ်ပြီး ၎င်းသည် ချောမွေ့နေမည်ဖြစ်သည်။
အညွှန်းကိန်းဂရပ်သည် အလားတူပြသထားသည်။ အခြေသည် 1 ထက်နည်းသော်လည်း 0 ထက်ကြီးသောအခါတွင် ဂုဏ်သတ္တိများရှိသည်။ ၎င်း၏ဂုဏ်သတ္တိများတွင် တစ်ခုတည်းသောပြောင်းလဲမှုမှာ ဂရပ်ကို လျော့ကျစေမည်ဖြစ်သည်။ Exponential graphs များကို exponential functions များမှရရှိသော data များကိုကိုယ်စားပြုရန်အသုံးပြုသည်။ ဒေတာအမျိုးအစားများနှင့် အညွှန်းကိန်းလုပ်ဆောင်ချက်များ၏ အသုံးချပုံကို ယခင်က ဆွေးနွေးခဲ့ပြီးဖြစ်သည်။
အညွှန်းကိန်းနှင့် လေးပုံတစ်ပုံ လုပ်ဆောင်ချက်များအကြား ကွာခြားချက် (အကြောင်းအရာကို ဤနေရာတွင် ဇယားတစ်ခုအနေဖြင့် အသုံးပြုပါ)
ယခုအခါတွင် စတုထ္တုတန်းနှင့် ပတ်သက်၍ ကောင်းစွာနားလည်သဘောပေါက်လာစေရန်၊ ဤအလွန်အရေးကြီးသောလုပ်ဆောင်ချက်နှစ်ခုအကြား ခြားနားချက်များကို ကျွန်ုပ်တို့ ဆွေးနွေးပါမည်။
| လေးပုံတစ်ပုံလုပ်ဆောင်ချက် | Exponential Function |
|---|---|
| ကိန်းရှင်သည် အခြေခံဖြစ်ပြီး ဖြစ်နိုင်ချေအမြင့်ဆုံးပါဝါမှာ (ax^2+bx+c))။ | အခြေခံသည် ကိန်းသေတစ်ခုဖြစ်ပြီး ထိုအခြေခံ၏ပါဝါသည် ကိန်းရှင်တစ်ခုဖြစ်သည်။ |
| ပြောင်းလဲမှုနှုန်းသည် စဉ်ဆက်မပြတ်ဖြစ်သည်၊ ဆိုလိုသည်မှာ ဂရပ်သည် စဉ်ဆက်မပြတ်နှုန်းဖြင့် တိုးလာသောကြောင့် အချို့သောအချိန်ကာလအတွင်း ဂရပ်၏ပြောင်းလဲမှုကို တွက်ချက်ရန် လွယ်ကူပါသည်။ | တစ်ခုအတွင်း၊ exponential လုပ်ဆောင်ချက်၊ ပြောင်းလဲမှုနှုန်းသည် သူ့ဘာသာသူ အချိုးကျနေပြီး ဂရပ်သည် တိုးနှုန်းတစ်ခုဖြင့် တိုးလာပါသည်။ |
| လေးပုံတစ်ပုံ ဂရပ်ပုံစံသည်အတက်အကျ သို့မဟုတ် အောက်ဘက်သို့ ထောင့်စွန်းသို့ရောက်ရှိသည့်အခါ အညွှန်းကိန်းများ။ | ထပ်ကိန်းဂရပ်တစ်ခုသည် အပေါ် သို့မဟုတ် အောက်သို့ ဦးတည်ချက်တစ်ခုသို့ ဆက်လက်ကျဆင်းနေပါမည်။ |
| လေးပုံတစ်ပုံ ဂရပ်မျဉ်းကွေးတစ်ခု ၎င်း၏ အမြင့်ဆုံး သို့မဟုတ် အနိမ့်ဆုံးအမှတ်သို့ ရောက်သောအခါ။ | အညွှန်းကိန်းဂရပ်တစ်ခုသည် အစမှစတင်၍ မျဉ်းကွေးအတိုင်း ဆက်သွားနေပါသည်။ |
Quadratic Function နှင့် Exponential Function
နိဂုံး
နှစ်ခုကြား ခြားနားချက်ကို အပြည့်အ၀ နားလည်ရန် အတိုချုံး ရှင်းလင်းချက်
အနှစ်ချုပ်ပြောရလျှင် Quadratic function နှင့် Exponential functions များသည် ၎င်းတို့၏ application နှင့် ၎င်းတို့၏ concept တွင် တစ်ခုနှင့်တစ်ခု ကွဲပြားပါသည်။ ကိန်းဂဏန်း လုပ်ဆောင်ချက်သည် စဉ်ဆက်မပြတ် တိုးလာမှုကို ညွှန်ပြသော်လည်း လေးထောင့်ကိန်း လုပ်ဆောင်ချက်သည် ၎င်း၏ မူလအဆင့် သို့မဟုတ် ဂရပ်၏ အစတွင် အရေအတွက် ကုန်ဆုံးသွားသည့် တိုးလာခြင်းနှင့် လျော့ကျခြင်းတို့ကို ညွှန်ပြသည်။
ဤဆောင်းပါး၏ အဓိကအင်္ဂါရပ်များနှင့် နိဂုံးချုပ်ထားသည်။ လုပ်ဆောင်ချက်တွေရော သူတို့ရဲ့ ကွဲပြားမှုတွေရော။ ဤလုပ်ဆောင်ချက်နှစ်ခုစလုံးသည် သင်္ချာနယ်ပယ်တွင် အလွန်အရေးပါပြီး သိပ္ပံ၊ ကူးသန်းရောင်းဝယ်ရေးနှင့် ကျွန်ုပ်တို့၏နေ့စဉ်ဘဝများကဲ့သို့သော နယ်ပယ်အသီးသီးတွင် အသုံးချလျက်ရှိသည်။ ထို့ကြောင့်၊ ဤလုပ်ဆောင်ချက်နှစ်ခုကို နက်နဲစွာနားလည်သဘောပေါက်ပြီး ကျွမ်းကျင်ပိုင်နိုင်စွာလုပ်ဆောင်ရန် ကျွန်ုပ်တိုက်တွန်းလိုပါသည်။
ဤဆောင်းပါးကိုဖတ်ရှုပြီးနောက်၊ ဤနှစ်ခုကိုဖြေရှင်းပုံ၊ ၎င်းတို့၏ကွာခြားချက်များ၊ ဂရပ်များကို သင်ရှင်းလင်းစွာနားလည်နိုင်လိမ့်မည်ဟုမျှော်လင့်ပါသည်။ , နှင့်အများကြီးပို. သင်္ချာနဲ့ပတ်သက်တဲ့ ဆောင်းပါးတစ်ပုဒ်က ပျင်းစရာလို့ထင်ရပေမယ့် ဒီစာကိုဖတ်ပြီးရင် သင်ဖတ်မိမှာပါ။နည်းမှန်လမ်းမှန်ဖြင့် ပေးပို့ပါက သင်္ချာပင် စိတ်ဝင်စားဖွယ်ကောင်းကြောင်း သဘောပေါက်ထားပါသည်။

