චතුරස්රාකාර සහ ඝාතීය ශ්රිතය අතර වෙනස කුමක්ද? (වෙනස පැහැදිලි කර ඇත) - සියලු වෙනස්කම්
අන්තර්ගත වගුව
ඔබ 9 වැනි හෝ 11 වැනි ශ්රේණියේ දී ඔබේ විෂය නිර්දේශයේ කොටසක් ලෙස චතුරස්ර සහ ඝාතීය ශ්රිත අධ්යයනය කර ඇත. කෙසේ වෙතත්, ඔබේ විෂය නිර්දේශයේ කොටසක් ලෙස මෙම කාර්යයන් අධ්යයනය කිරීමෙන් ඔබට මේ දෙක අතර වෙනස පිළිබඳ පැහැදිලි අවබෝධයක් අවශ්ය නොවේ.
ඔබේ විෂය නිර්දේශයේ කොටසක් ලෙස, ඔබට අවශ්ය වන්නේ මේ දෙක සහ ඒවායේ යෙදුම් අතර ඇති විය හැකි වෙනස්කම් ගැන කිසිවිටෙක අනුමාන නොකර ඒ දෙකට අදාළ සමීකරණ සහ ගැටලු විසඳීමට පමණි.
ඉතින් මේ ලිපියෙන් මම බලාපොරොත්තු වෙන්නේ ප්රස්තාර, සමීකරණ සහ උදාහරණ ආශ්රයෙන් මේ දෙකේ වෙනස ඔබට පහසුවෙන් අවබෝධ කර ගැනීමට හැකි වන පරිදි දැනුවත් කිරීමයි.
බලන්න: Bō VS Quarterstaff: වඩා හොඳ ආයුධය කුමක්ද? - සියලු වෙනස්කම්අපි පටන් ගනිමු.
ගණිතයේ කාර්යය යනු කුමක්ද?
ගණිතයේ ශ්රිතයක් වඩාත් හොඳින් අර්ථ දැක්වෙන්නේ එක් එක් ආදානයට එකම ප්රතිඵලයක් ඇති යෙදවුම් අතර සම්බන්ධතාවයක් ලෙසයි, එයින් අදහස් වන්නේ එක් එක් ආදානය එකම ප්රතිදානය ලබා දෙන බවයි.
ගණිතයේ ශ්රිතයක් බොහෝ විට f(x) මගින් හෝ නිරූපණය කෙරේ. උදාහරණයක් ලෙස f(x)=x^2. මෙම ශ්රිතය අපට වරහනේ ඇති සංඛ්යාවේ වර්ගය ලබා දෙනු ඇත, මෙම අවස්ථාවෙහිදී, අංක 2.
මෙය ශ්රිතයේ ආදානය කුමක් වුවත් අපට එම ප්රතිදානයම ලබා දේ. මෙම අවස්ථාවෙහිදී, එය සෑම විටම ප්රතිදානය ලෙස වරහනේ ඇති සංඛ්යාවේ වර්ගය ආපසු ලබා දෙනු ඇත.
විවිධ කාර්යයන් ඉටු කිරීමට භාවිතා කරන විවිධ කාර්යයන් ගණිතයේ ඇති අතර ඒවා විවිධ ක්ෂේත්රවල යෙදේ. කෙසේ වෙතත්, අපි සාකච්ඡා කිරීමට යන කාර්යයන්මෙම ලිපියේ චතුරස්රාකාර සහ ඝාතීය ශ්රිත වේ. මෙම ශ්රිත දෙක අතර වෙනස ඉස්මතු කිරීමට අපි ප්රධාන වශයෙන් අවධානය යොමු කරමු.
චතුර්ශ්රිත ශ්රිතයක් යනු කුමක්ද?
චතුරශ්රිත ශ්රිතයක් බහුපද ශ්රිතයක් වන අතර එය ax^2+bx+c සමීකරණයේ ඕනෑම ආකාරයකි. උපරිම ඝාතකය 2 විය හැකි නිසා එය අංශක 2 හි බහුපදයක් ලෙසද හැඳින්වේ.
චතුරස්ර සූත්රය ඉංජිනේරු වැනි විද්යාවේ විවිධ ක්ෂේත්රවල භාවිතා වේ. එය පරාලයක් හරහා චිත්රක ලෙස නිරූපණය කෙරේ.
මෙම පැරබෝලා අපගේ එදිනෙදා ජීවිතයේ බෝලයක් විසි කිරීම හෝ ගොල්ෆ් පන්දුවකට පහර දීම වැනි විවිධ ක්රියාකාරකම් සඳහා භාවිතා වේ. මිනුම්වල නැති වූ විචල්යයන් සෙවීමට සහ ඕනෑම වස්තුවක ප්රවේගය සොයා ගැනීමට සහ වාණිජ ක්ෂේත්රයේ ඕනෑම භාණ්ඩයක හෝ භාණ්ඩයක ලාභය ගණනය කිරීමට චතුරස්ර සමීකරණ භාවිතා වේ.
මෙන්න චතුරස්ර සමීකරණයක උදාහරණයක්: 3x^ 2+5x+9 a:3 b:5 c:9
මෙය එහි සම්මත ස්වරූපයෙන් චතුරස්ර ශ්රිතයක උදාහරණයකි. එවැනි සමීකරණ විසඳීම සඳහා භාවිතා කරන සූත්රය චතුරස්ර සූත්රය ලෙස හැඳින්වේ, එය පහත දැක්වේ: (-b±√(b²-4ac))/(2a).
ඝාතීය ශ්රිතයක් යනු කුමක්ද?
ගණිතයේ ඝාතීය ශ්රිතයක් යනු f(x)=a^x ආකාරයෙන් ඇති ශ්රිතයක් වන අතර එහිදී a පාදය වේ, එය නියතයක් වන අතර එය සැමවිටම 0 ට වඩා වැඩි විය යුතුය. f(x)=\exp හෝ e^{x} මගින් දක්වනු ලැබේ.
වඩාත්ම බහුලව භාවිතා වන ඝාතීය පදනම e යනු ස්වභාවික ලෙස හැඳින්වේ.ලඝුගණකය. එය ජනගහනය සහ බැක්ටීරියා වැනි විවිධ දේවල වර්ධන වේගය ගණනය කිරීමට භාවිතා කරයි. ඝාතීය ශ්රිතයක් ගණිතයේ වැදගත්ම ශ්රිතය ලෙස විවාද කළ හැක.
එය ඉතා වැදගත් වන්නේ එය විවිධ ක්ෂේත්රවල භාවිතා වන බැවිනි:
- විද්යාව
- වාණිජ්යය.
උදාහරණයක් ලෙස, ඔබ බැංකුවක තැන්පත් කරන මුදල් සඳහා පොලී අනුපාතය ඝාතීය ලෙස වැඩි වන අතර එයින් අදහස් වන්නේ එය ඝාතීය වක්රයක් අනුගමනය කරන බවයි, එය ඝාතීය ශ්රිත භාවිතයෙන් ගණනය කළ හැක.
එපමනක් නොව, ණය වර්ධනය ද ඝාතීය ලෙස වැඩි වන අතර ඝාතීය වක්රයක් අනුගමනය කරයි, එබැවින්, ඝාතීය ශ්රිත භාවිතා කිරීමෙන් ඔබට ඔබේ ණය ඉහළ යාම නැවැත්විය හැකි අතර ඔබේ මූල්ය පාලනය කෙරෙහි වැඩි පාලනයක් තිබිය හැකිය.
ජීව විද්යාවේදී, එය නිශ්චිත කාලපරිච්ඡේදයක් තුළ නිශ්චිත ප්රදේශයක ජනගහන වර්ධනය ඇස්තමේන්තු කිරීමට භාවිතා කරයි.
බලන්න: ජීරා ඇට සහ දුරු ඇට අතර වෙනස කුමක්ද? (ඔබේ කුළුබඩු දැනගන්න) - සියලු වෙනස්කම්යුරේනියම් දිරාපත්වීම වැනි විකිරණශීලීතාව ද ඝාතීය වර්ධනයක් අනුගමනය කරයි. මේ අනුව, මෙය ඝාතීය ශ්රිතයේ තවත් යෙදුමකි.
භෞතික විද්යාවේදී, sin, cos, sound waves, සහ වෙනත් බොහෝ තරංග වැනි සියලුම තරංග ඝාතීය ශ්රිතයන් අනුවද ලිවිය හැක, එබැවින් මෙම ශ්රිතය භෞතික විද්යාඥයින්ට මෙම තරංග පිළිබඳ පර්යේෂණ කිරීමට උපකාර කරයි.
කුමක්ද? චතුරස්ර ප්රස්තාරයක් ද?

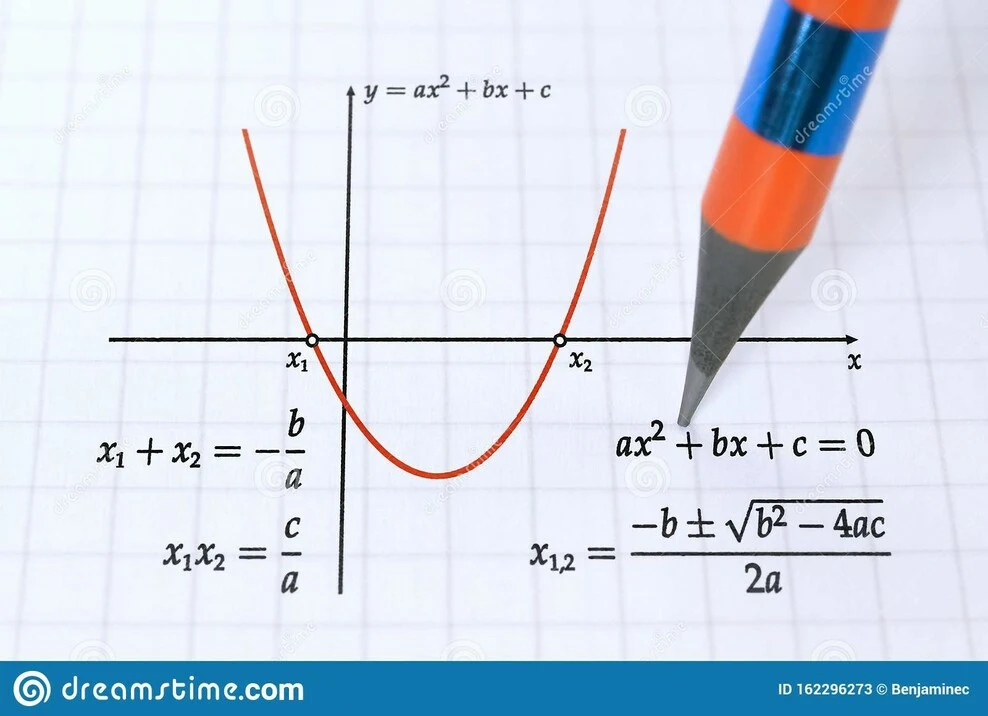
මෙය චතුරස්ර ප්රස්ථාරයක නිරූපණයකි
චතුරශ්රිත ශ්රිතයක ප්රස්ථාරය ඉහත පින්තූරයේ දැක්වෙන පරිදි U-හැඩැති පරාලයකි. මෙම පැරබෝලා සිනහවක් මෙන් විවෘත විය හැකිය, නැතහොත් නළල රැලි ගැසීමක් මෙන් පහළට විවෘත විය හැකිය. එමපැරබෝලා විවෘත වන ආකාරය සංගුණකය මත රඳා පවතී: "a" ax^2+bx+c සමීකරණයේ. සංගුණකය a>0 නම්, පරාවලය විවෘත වන අතර සංගුණකය a<0 නම්, පරාවලය පහළට විවෘත වේ.
- පැරබෝලාවක ඉහළම හෝ පහළම ලක්ෂ්යය ශීර්ෂය ලෙස හැඳින්වේ.
- ශීර්ෂය නියෝජනය කරන ලක්ෂ්යය, උපරිම හෝ අවම වේවා පරාවලය විවෘත වන ආකාරය මත රඳා පවතී.
එය විවෘත වුවහොත් එම සිරස් ප්රස්ථාරයේ අවම ලක්ෂ්යය නියෝජනය කරයි. පහළට විවෘත වන අතර එවිට සිරස් චතුරස්ර ප්රස්ථාරයේ උපරිම ලක්ෂ්යය නියෝජනය කරයි. පැරබෝලා වල තවත් ලක්ෂණයක් වන්නේ සිරස් රේඛාවක් වන සමමිතික රේඛාව වන අතර එය සිරස් රේඛාවක් වන අතර එය සමාන හා සමාන අර්ධ 2 කට බෙදීමට භාවිතා කරයි.
පහත සූත්රය භාවිතා කිරීමෙන් එය ලබා ගත හැක: y =a(x−h)2+k. චතුරස්ර ප්රස්ථාරයට y-අන්තර්ඡේදනයක් ඇත, එය පරාවලය y-අක්ෂය ඡේදනය කරන ලක්ෂ්යය වේ. මෙම y-අන්තර්ඡේදනයට ඇත්තේ එක් අගයක් පමණි, එනම් පරාවලය y අක්ෂය එක් වරක් පමණක් ඡේදනය කරයි. x-අන්තර්ඡේදනය යනු පරාවලය x-අක්ෂය හරස් කරන හෝ හරස් කරන ලක්ෂ්යය වේ.
අන්තරාවර්තන සංඛ්යාව 0, 1, හෝ 2 විය හැක. චතුරස්ර සමීකරණයකට පමණක් කළ හැකි නිසා උපරිම අන්තර් නිරෝධ ගණන 2 වේ. විසඳුම් 2 ක් හෝ මුල් 2 ක් දක්වා ඇත. චතුරස්රාකාර ප්රස්තාරය යනු චතුරස්රාකාර සමීකරණ විසඳීමේ එක් ක්රමයකි. එය චතුරස්රාකාර සමීකරණ විසඳීමේ චිත්රක ක්රමය ලෙස හැඳින්වේ.
චතුරස්රාකාර ප්රස්තාරය භාවිතා වේඅපගේ දෛනික ජීවිතයේ බොහෝ ක්ෂේත්ර ප්රධාන වශයෙන් ක්රීඩා වේ. පන්දුවක් විසි කිරීම හෝ උස් වේදිකාවකින් පැනීම, චතුරස්ර ප්රස්ථාරයකින් නිරූපණය කළ හැකි අවස්ථා සඳහා උදාහරණ වේ. එවිට පන්දුව හෝ පුද්ගලයා ළඟා වූ උපරිම හෝ අවම ලකුණු සොයා ගැනීමට චතුරස්ර ප්රස්ථාරය භාවිතා කළ හැක.
ඝාතීය ප්රස්ථාර මොනවාද?
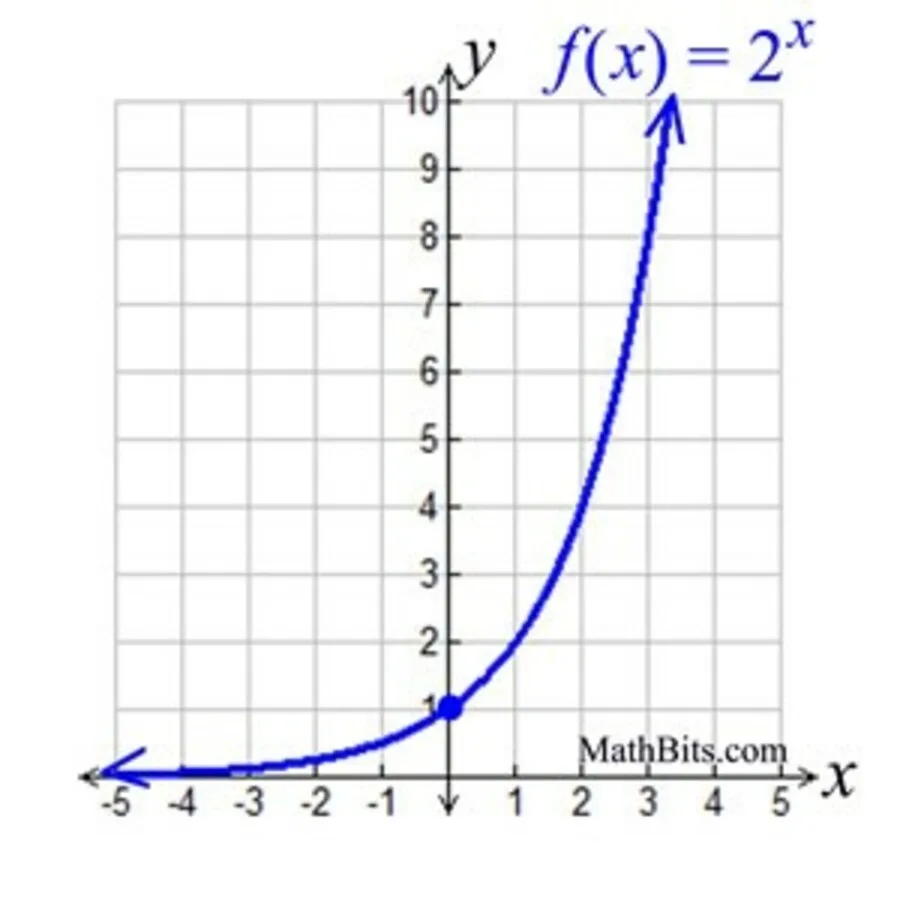
මෙය ඝාතීය ප්රස්ථාරයක නිරූපණයකි
වීජීය සහ ලෝකෝත්තර සමීකරණ දෙකම ගණක යන්ත්රයක් ආධාරයෙන් බොහෝ විට අතින් විසඳිය හැක, කෙසේ වෙතත්, මෙම සමීකරණ දෙක, වීජීය සහ ලෝකෝත්තර එකට පෙනී සිටින අතර, ඒවා අතින් විසඳීම ඉතා අපහසු හෝ කළ නොහැකි දෙයක් බවට පත්වේ. එබැවින් මෙම සමීකරණ දෙක එකට විසඳීම සඳහා, අපි ඝාතීය ප්රස්ථාරය භාවිතා කර එය චිත්රක ලෙස විසඳන්නෙමු.
සරලම ඝාතීය ශ්රිතය වන්නේ f(x) = ax, a>0, a≠1. මෙම ශ්රිතයේ දී, a පාදය සැමවිටම 0 ට වඩා විශාල ලෙස තබා ඇත, මන්ද පාදය 0 ට වඩා අඩු නම්, එය අපට යථාර්ථවාදී සංඛ්යාවක් ලබා දිය හැකි බැවිනි.
පාදය 1 නම්, එහි ඝාතකය නොසලකා එය සැමවිටම 1 ආපසු ලබා දෙන අතර එය ඉතා නීරස කාර්යයක් බවට පත් වනු ඇත. මෙම හේතූන් නිසා ඝාතීය ශ්රිතයට යම් සීමාවන් පනවා ඇත.
ඝාතීය ශ්රිතයක ප්රස්ථාරය පාදය 1 ට වඩා වැඩි ද 1 ට අඩු නමුත් 0 ට වඩා වැඩි ද යන්න මත පදනම්ව විවිධ ගුණාංග පෙන්වයි. පදනම ඇති විට පහත ගුණාංග සංදර්ශන කරන්න1 ට වඩා විශාල විය යුතුය. වසම තාත්වික සංඛ්යා වලින් පමණක් සමන්විත වනු ඇත, පරාසය y>0 වනු ඇත, ප්රස්ථාරය නිරන්තරයෙන් වැඩි වනු ඇත, ප්රස්ථාරය අඛණ්ඩව පවතින අතර එය සුමට වනු ඇත.
ඝාතීය ප්රස්ථාරය සමාන වේ පාදය 1 ට වඩා අඩු නමුත් 0 ට වඩා විශාල වන විට ගුණාංග. එහි ගුණාංගවල එකම වෙනස වන්නේ ප්රස්ථාරය අඩු වීමයි. ඝාතීය ශ්රිත හරහා ලබාගත් දත්ත නිරූපණය කිරීමට ඝාතීය ප්රස්ථාර භාවිතා වේ. දත්ත වර්ග සහ ඝාතීය ශ්රිතවල යෙදීම් මීට පෙර සාකච්ඡා කර ඇත.
ඝාතීය සහ චතුර්ශ්රිත ශ්රිත අතර වෙනස (මෙහි අන්තර්ගතය වගුවක් ලෙස භාවිතා කරන්න)
දැන් චතුරස්ර සහ ඝාතීය ශ්රිත වර්ධනය කර ඇත. මෙම ඉතා වැදගත් ශ්රිත දෙකක් අතර ඇති වෙනස්කම් අපි සාකච්ඡා කරමු.
| චතුශ්රිත ශ්රිතය | ඝාතීය ශ්රිතය | විචල්යය පාදය වන අතර හැකි ඉහළම බලය (ax^2+bx+c) වේ. | පාදය නියතයක් වන අතර එම පාදයේ බලය විචල්යයකි. |
|---|---|
| වෙනස් වීමේ වේගය නියත වන අතර එයින් අදහස් වන්නේ ප්රස්ථාරය නියත වේගයකින් වැඩි වන අතර එම නිසා නිශ්චිත කාල සීමාවක් තුළ ප්රස්ථාරයේ වෙනස ගණනය කිරීම පහසුය. | ක ඝාතීය ශ්රිතය, වෙනස් වීමේ වේගය එයට සමානුපාතික වන අතර ප්රස්ථාරය වැඩිවන වේගයකින් වැඩි වේ. |
| චතුරස්ර ප්රස්ථාරය සාදයිparabola එය ඉහළට හෝ පහළට දිශාවට ශීර්ෂයට ළඟා වන විට. | ඝාතීය ප්රස්ථාරයක් ඉහළට හෝ පහළට එක් දිශාවකට දිගටම වැටේ. |
| චතුරස්ර ප්රස්තාර වක්ර එය එහි උපරිම හෝ අවම ලක්ෂ්යයට ළඟා වූ විට. | ඝාතීය ප්රස්ථාරයක් ආරම්භයේ සිටම වක්ර වේ. |
චතුශ්රිත ශ්රිතය එදිරිව ඝාතීය ශ්රිතය
නිගමනය
ඒ දෙක අතර වෙනස සම්පූර්ණයෙන් අවබෝධ කර ගැනීම සඳහා කෙටි පැහැදිලි කිරීමක්
සාරාංශගත කිරීම සඳහා, චතුර්ශ්රිත ශ්රිත සහ ඝාතීය ශ්රිතයන් ඒවායේ යෙදුම සහ ඒවායේ සංකල්පය තුළ එකිනෙකට වෙනස් වේ. ඝාතීය ශ්රිතයක් අඛණ්ඩ වැඩි වීමක් පෙන්නුම් කරන අතර චතුර්ශ්රිත ශ්රිතයක් මඟින් ප්රමාණය එහි මූලාරම්භයේ මට්ටමින් හෝ ප්රස්ථාරයේ ආරම්භයේ දී අවසන් වන වැඩි වීමක් සහ අඩුවීමක් පෙන්නුම් කරයි.
මෙම ලිපිය අවසන් වන්නේ ප්රධාන ලක්ෂණ සමඟිනි. කාර්යයන් මෙන්ම ඒවායේ වෙනස්කම් දෙකම. මෙම කාර්යයන් දෙකම ගණිත ක්ෂේත්රයේ අතිමහත් වැදගත්කමක් ඇති අතර විද්යාව, වාණිජ්යය සහ අපගේ දෛනික ජීවිතය වැනි විවිධ ක්ෂේත්රවල ද අදාළ වේ. එමනිසා, මෙම කාර්යයන් දෙක පිළිබඳ ගැඹුරු අවබෝධයක් සහ ප්රවීණත්වයක් වර්ධනය කර ගැනීමට මම ඔබව දිරිමත් කරමි.
මෙම ලිපිය කියවීමෙන් පසු, මෙම දෙක විසඳන ආකාරය, ඒවායේ වෙනස්කම්, ප්රස්තාර පිළිබඳව ඔබට පැහැදිලි අවබෝධයක් ලැබෙනු ඇතැයි අපේක්ෂා කරමු. , සහ තවත් බොහෝ දේ. ගණිතයට සම්බන්ධ ලිපියක් නීරස බවක් පෙනුනත් මෙය කියවීමෙන් පසු ඔබට එය නීරස වනු ඇතනිවැරදි ආකාරයෙන් ලබා දෙන්නේ නම් ගණිතය පවා රසවත් විය හැකි බව අවබෝධ කරගෙන ඇත.

