d2y/dx2=(dydx)^2의 차이점은 무엇입니까? (설명) – 모든 차이점
목차
도함수는 과학, 공학, 물리학 등의 과목을 포함하여 수학 및 일상 생활 외에 많은 용도로 사용됩니다.
이전 과정에서 삼각법, 암시적, 로그 등을 포함하여 다양한 함수의 도함수를 계산하는 능력을 마스터해야 합니다.
d2y/dx2 및 (dydx)^2는 두 도함수입니다. 방정식. 그러나 그것들을 이해하기 위해서는 먼저 2차 도함수가 정확히 무엇인지 이해해야 합니다.
미적분학에서 함수의 도함수는 2차 도함수로 알려져 있으며 때로는 2차 도함수라고도 합니다.
2차 미분은 대략적으로 말하면 양의 변화율 자체가 어떻게 변하는지를 측정합니다. 예를 들어, 시간에 대한 물체 위치의 2차 도함수는 물체의 순간 가속도 또는 물체의 속도가 시간에 따라 변하는 비율입니다.
이 기사에서는 는 d2y/dx2=(dydx)^2와 정확히 미분의 의미 사이의 차이입니다.
D2y/dx2 Vs (dydx)^2
dy/dx의 미분(이 2는 인덱스 표기법처럼 보일 수 있지만 그렇지 않습니다. 반면에 (dydx)2는 1차 미분의 제곱입니다.
예:
Take Y=3 ???? 3 +6 ???? 2y=3×3+6×2
1차 도함수: dy/dx=9 ???? 2+12 ???? dydx=9×2+12x
2차 도함수:d2yd????2=18 ???? +12d2ydx2=18x+12
1차 미분의 제곱: (dydx)2=(9 ??? ? 2+12 ???? )2=(81 ???? 4+216 ???? 3+144
2차 도함수란 무엇입니까?
도함수를 미분하면 2차 도함수를 얻습니다. dy/dx는 x에 대한 y의 도함수임을 기억하십시오. 2차 도함수는 발음됩니다. "dee two y x d x squared"는 d2y/dx2로 표시됩니다.
정지점의 특성은 2차 도함수(최대점, 최소점, 또는 변곡점).
dy/dx = 0일 때 곡선은 정지점에 도달합니다. 정지점의 유형(최대, 최소 또는 변곡점)은 일단 2차 도함수를 사용하여 결정할 수 있습니다. 정지점의 위치가 설정되었습니다.
| d2y/d2x=Positive | 최소점입니다 |
| d2y/d2x=음수 | 최대점입니다 |
| d2y/d2x는 0과 같습니다 | 최소점과 최대점 모두입니다 |
| d2y/d2x=0 | 이전 고정점 섹션에서와 같이 고정점 양쪽에서 dy/dx 값을 테스트합니다. |
최대점과 최소점을 어떻게 식별합니까?

d2y/d2x는 2차 미분입니다.
또한보십시오: 라이트 베이스와 액센트 베이스 페인트의 차이점은 무엇입니까? (설명) – 모든 차이점미분이란 무엇입니까?
수학에서 실수 변수의 함수의 도함수는인수(입력 값)의 변화에 대한 함수 값(출력 값)의 민감도. 미적분학의 핵심 도구는 미분입니다.
예를 들어 항목의 속도는 시간에 대한 위치의 파생물입니다. 시간이 지남에 따라 물체의 위치가 얼마나 빨리 변하는지 정량화합니다.
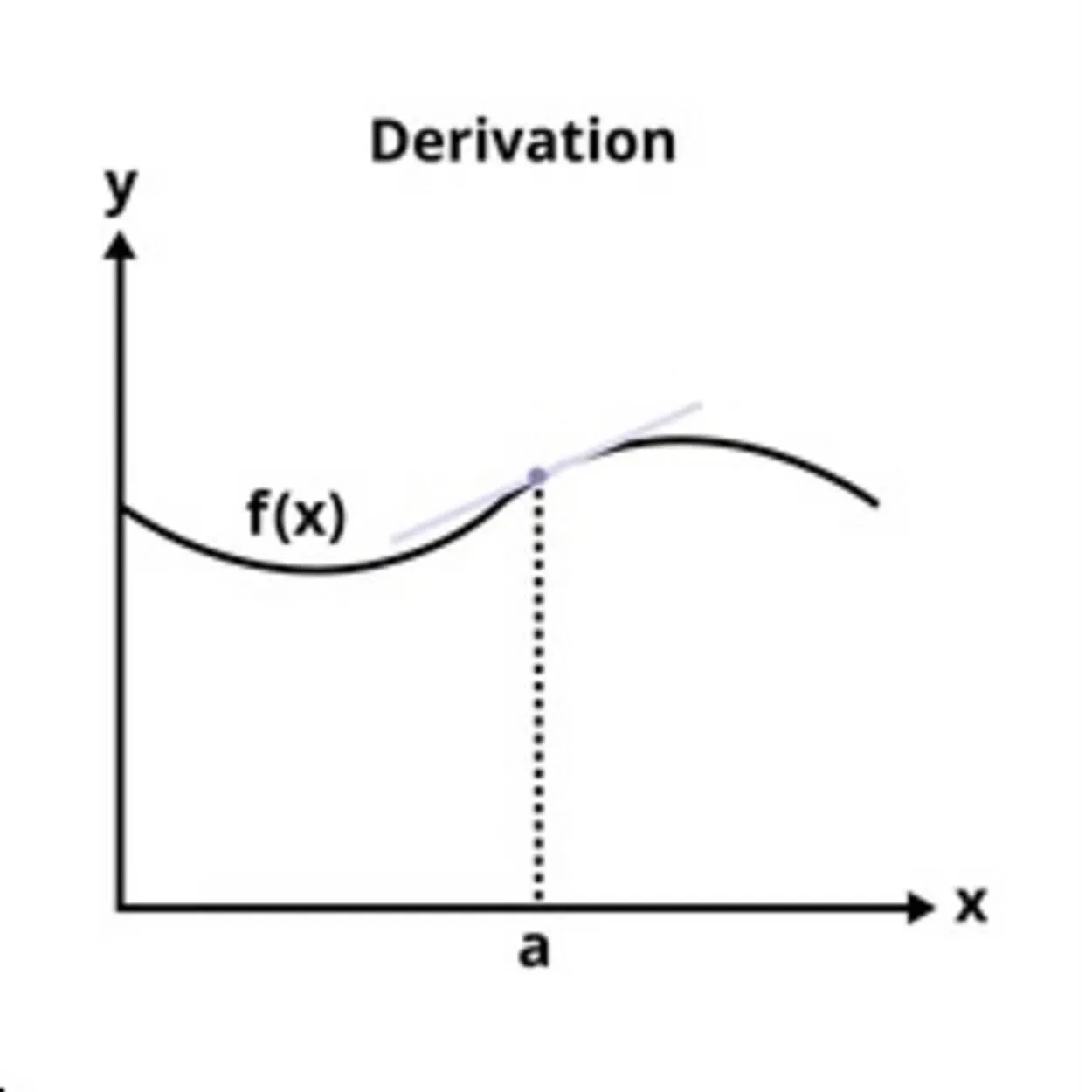
발생할 때 주어진 입력 값에서 함수의 그래프에 대한 접선의 기울기는 단일 변수의 함수의 도함수입니다. 해당 입력 값에 가장 가까운 함수는 접선에 의해 선형적으로 가장 잘 근사됩니다.
이 때문에 미분을 독립변수의 순간변화에 대한 종속변수의 순간변화의 비율인 '순간변화율'이라고도 한다.
여러 실제 변수의 함수를 포함하기 위해 미분을 일반화할 수 있습니다. 이 일반화는 도함수를 선형 변환으로 재해석합니다. 해당 그래프는 적절한 변환 후 원래 함수의 그래프에 대한 최상의 선형 근사치입니다.
또한보십시오: "Ser"와 "Ir"의 차이점은 무엇입니까? (설명) – 모든 차이점독립변수와 종속변수의 선택이 제공하는 기반에 대해 자코비 행렬은 이러한 선형변환을 나타내는 행렬이다.
독립변수의 편도함수를 이용하여 계산할 수 있다. 그래디언트 벡터는 실수 값 함수에 대한 야코비 행렬을 여러변수.
미분은 미분을 찾는 작업입니다. Antidifferentiation은 반대 과정에 대한 용어입니다. 미분과 적분은 미적분 기본 정리와 관련이 있습니다. 단일 변수 미적분학의 두 가지 기본 연산은 미분과 적분입니다.
실수 변수의 미분과 함수에 대해 알아보려면 이 비디오를 시청하십시오.
다양한 표기법
라이프니츠의 표기법
1675년 Gottfried Wilhelm Leibniz는 문자 dx, dy 및 dy/dx를 도입했습니다. 오늘날에도 방정식 y = f(x)에서 종속 변수와 독립 변수 간의 관계가 기능적이라고 간주될 때 자주 사용됩니다.
미분 변수(분모에서)는 부분 미분에 중요한 Leibniz의 표기법을 사용하여 지정해야 합니다.
Lagrange의 표기법
가장 인기 있는 현대 미분 표기법 중 하나인 소수 표기법이라고도 하며 소수 표기법과 Joseph-Louis Lagrange의 작품입니다. 이것은 함수 f의 도함수를 f1로 나타냅니다. 후자의 표기법은 일반화하여 f의 n차 도함수에 대한 표기법 f(n)을 제공합니다. 이것은 도함수를 함수로 논의할 때 더 편리합니다. 이 상황에서 라이프니츠 표기법은 복잡할 수 있기 때문에 자체 함수가 아니라
뉴턴의 표기법
점은시간 도함수를 나타내기 위해 종종 "점 표기법"으로 알려진 뉴턴의 미분 표기법에서 함수 이름 위에 배치됩니다.
시간 또는 호 길이와 관련된 도함수만 이 표기법을 사용하여 표시됩니다. 일반적으로 미분 기하학 및 물리학의 미분 방정식에 적용됩니다. 단, 점 표기법은 여러 독립변수와 고차 도함수(차수가 4 이상)에는 적용할 수 없다. 함수 f에 적용하여 오일러 표기법의 D. Dnd는 n번째 도함수를 나타냅니다.
y = f(x)가 종속변수인 경우 독립변수 x는 D에 첨자 x를 추가하여 자주 명확해집니다.
변수 x가 이해될 때 , 예를 들어 이것이 방정식에 포함된 유일한 독립 변수인 경우 이 첨자는 자주 생략됩니다.
선형미분방정식의 표현과 풀이에는 오일러의 표기법이 도움이 된다.
수학에서의 미분의 응용
미분은 수학에서 자주 사용된다. 함수의 최대값 또는 최소값, 곡선의 기울기 또는 변곡점을 결정하는 데 사용할 수 있습니다.
다음은 파생 상품을 사용할 몇 가지 예입니다. 다음 섹션에서는 각각에 대해 자세히 설명합니다. 파생 상품의 적용
- 양의 변화율 계산
- 값의 적절한 추정치 얻기
- 곡선의 접선 및 법선에 대한 방정식 찾기
- 변곡점, 최대값 및 최소값 식별
- 증가 및 감소 함수 평가
점을 계산하기 위해 도함수 사용 변곡점, 최대점과 최소점
파생상품의 실생활 적용
미분상품은 실생활에서 다양한 상황에서 사용될 수 있습니다. 다음은 파생을 사용할 수 있는 몇 가지 상황 목록입니다.
- 비즈니스에서 손익을 계산합니다.
- 온도 변화를 측정하기 위해.
- 시속 마일, 시속 킬로미터 등과 같은 이동 속도를 계산하려면
- 미분을 사용하여 수많은 물리 방정식을 도출합니다.
- 지진 규모 범위를 찾는 것은 지진학 연구에서 가장 좋아하는 작업입니다.
결론
- d2y/dx2는 두 번째 파생입니다.
- (dy/dx) ^2는 1차 미분의 제곱이다.
- 미분은 실생활에서 여러 가지 목적으로 다양한 분야에서 사용된다.
- 미분은 다음에서 사용된다. 최대 및 최소 포인트를 계산하는 수학.
- 비즈니스에서 비즈니스의 재정을 계산하고 손익을 계산하는 데 사용할 수 있습니다.

