Mis on erinevus d2y/dx2=(dydx)^2? (Selgitatud) - Kõik erinevused
Sisukord
Tuletisi kasutatakse palju väljaspool matemaatikat ja igapäevaelu, sealhulgas sellistes valdkondades nagu teadus, inseneriteadus, füüsika ja muud.
Te peate olema varasemates kursustes omandanud erinevate funktsioonide tuletise arvutamise oskuse, sealhulgas trigonomeetrilise, implikatiivse, logaritmilise jne tuletise arvutamise oskuse.
d2y/dx2 ja (dydx)^2 on kaks tuletisvõrrandit. Kuid nende mõistmiseks tuleb kõigepealt mõista, mis on täpselt teine tuletis.
Funktsiooni tuletis on matemaatikas tuntud kui teine tuletis, mida mõnikord nimetatakse teise astme tuletiseks.
Teise tuletisega mõõdetakse üldjoontes seda, kuidas muutub suurus ise. Näiteks objekti asukoha teine tuletis aja suhtes on objekti hetkeline kiirendus ehk kiirus, mis muutub aja suhtes.
Selles artiklis räägin teile, mis vahe on d2y/dx2=(dydx)^2 ja mida täpselt tähendab tuletis.
D2y/dx2 Vs (dydx)^2
Derivaat dy/dx (Need 2s võivad näida nagu indeksite märkimine, kuid nad ei ole seda). (dydx)2 on seevastu esimese tuletise ruut.
Näide:
Võtame Y=3 ???? 3+6 ???? 2y=3×3+6×2
Esimene tuletis: dy/dx=9 ???? 2+12 ???? dydx=9×2+12x
Teine tuletis: d2yd????2=18 ???? +12d2ydx2=18x+12
Esimese tuletise ruut: (dydx)2=(9 ???? 2+12 ???? )2=(81 ???? 4+216 ???? 3+144
Mis on teine tuletis?
Kui te diferentseerite tuletist, saate teise tuletise. Pidage meeles, et dy/dx on y tuletis x suhtes. Teine tuletis, mida hääldatakse "dee kahe y poolt d x ruutu", esitatakse kui d2y/dx2.
Statsionaarsete punktide olemust on lihtsam kindlaks teha teise tuletise abil (kas tegemist on maksimum-, miinimum- või murdepunktidega).
Kui dy/dx = 0, saavutab kõver statsionaarse punkti. Statsionaarse punkti tüübi (maksimum, miinimum või murdepunkt) saab määrata teise tuletise abil, kui statsionaarse punkti asukoht on kindlaks tehtud.
| d2y/d2x=Positiivne | See on minimaalne punkt |
| d2y/d2x=Negatiivne | See on maksimaalne punkt |
| d2y/d2x võrdub nulliga | See on nii miinimum- kui ka maksimumpunkt |
| d2y/d2x=0 | Testige dy/dx väärtusi mõlemal pool statsionaarset punkti, nagu eelnevalt statsionaarseid punkte käsitlevas osas. |
Kuidas tuvastada maksimumi ja miinimumi punkte?

d2y/d2x on teine tuletis.
Mis on tuletis?
Reaalmuutuja funktsiooni tuletis kvantifitseerib matemaatikas funktsiooni väärtuse (väljundväärtuse) tundlikkust selle argumendi (sisendväärtuse) muutuste suhtes. Arvutuse põhiline tööriist on tuletis.
Eseme kiirus on näiteks tema asukoha tuletis aja suhtes. See näitab, kui kiiresti muutub eseme asukoht aja möödudes.
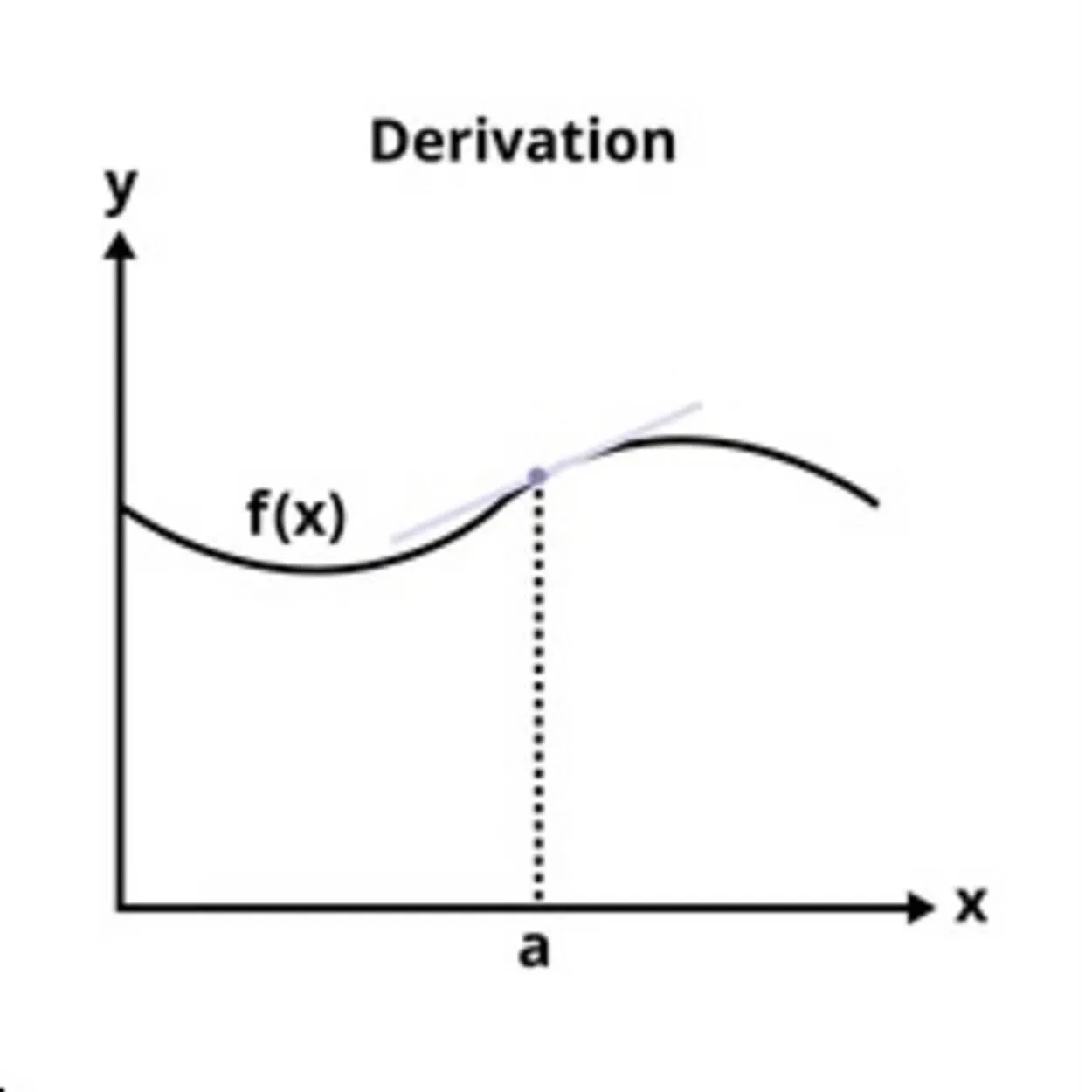
Kui see juhtub, siis on funktsiooni graafiku puutujajoone kalle antud sisendväärtuse juures ühe muutuja funktsiooni tuletis. Sellele sisendväärtusele kõige lähemal olev funktsioon on kõige paremini lähendatud lineaarselt puutujajoone abil.
Seetõttu nimetatakse tuletist sageli "hetkelise muutuse kiiruseks", mis on sõltuva muutuja hetkelise muutuse ja sõltumatu muutuja muutuse suhe.
Mitme reaalmuutuja funktsioonide hõlmamiseks saab tuletisi üldistada. See üldistus tõlgendab tuletist ümber lineaarseks teisenduseks, mille graafik on pärast sobivat teisendamist parim lineaarne lähendus algse funktsiooni graafikule.
Mis puutub sõltumatute ja sõltuvate muutujate valikuga antud alusesse, siis Jakobi maatriks on maatriks, mis kujutab seda lineaarset teisendust.
Seda saab arvutada, kasutades sõltumatute muutujate osalisi tuletisi. Gradientvektor asendab mitme muutujaga reaalväärtusliku funktsiooni puhul Jakobi maatriksit.
Diferentseerimine on tuletise leidmise toiming. Antidiferentseerimine on vastupidise protsessi nimetus. Antidiferentseerimine ja integratsioon on seotud arvutuse põhitõdes. Ühe muutuja arvutamise kaks põhilist operatsiooni on diferentseerimine ja integratsioon.
Vaadake seda videot, et teada saada reaalmuutuja tuletistest ja funktsioonist
Erinevad märked
Leibnizi märkimine
1675. aastal võttis Gottfried Wilhelm Leibniz kasutusele kirjad dx, dy ja dy/dx. Seda kasutatakse ka tänapäeval sageli, kui sõltuvate ja sõltumatute muutujate vahelist seost võrrandis y = f(x) käsitletakse funktsionaalsena.
Vaata ka: Erinevus kõrgresolutsiooniga Flac 24/96+ ja tavalise tihendamata 16-bitise CD vahel - kõik erinevusedDiferentseerimise muutuja (nimetaja) saab määrata Leibnizi notatsiooni abil, mis on oluline osalise diferentseerimise puhul.
Lagrange'i märkimine
Üks kõige populaarsemaid kaasaegseid diferentseerimise tähendusviise, mida mõnikord tuntakse ka kui priimusmärk, kasutab priimusmärki ja seda on omistatud Joseph-Louis Lagrange'ile. See tähistab funktsiooni f tuletist kui f1.
Viimane tähendus üldistus annab f(n) tähistamiseks f-i n-ndat tuletist, mis on mugavam, kui arutatakse tuletist kui funktsiooni, mitte kui funktsiooni iseendast, sest Leibnizi tähendus võib selles olukorras olla keeruline.
Newtoni märkimine
Newtoni diferentseerimise märkimisviisis, mida sageli tuntakse "punktmärkimisena", pannakse funktsiooni nime kohale punkt, et tähistada aja tuletist.
Selle notatsiooni abil esitatakse ainult aja või kaarepikkuse suhtes tuletisi. Tavaliselt kasutatakse seda diferentsiaalgeomeetria ja füüsika diferentsiaalvõrrandite puhul. Punktnotatsioon on aga mitmete sõltumatute muutujate ja kõrgema astme tuletiste (4. või enama astme) puhul mittekohaldatav.
Euleri notatsioon
Esimene tuletis Df saadakse Euleri notatsioonis oleva diferentsiaaloperaatori D abil, rakendades seda funktsioonile f. Dnd tähistab n-ndat tuletist.
Kui y = f(x) on sõltuv muutuja, selgitatakse sageli sõltumatut muutujat x, lisades D-le alajaotuse x.
Vaata ka: Holiday Inn VS Holiday Inn Express (erinevused) - Kõik erinevusedKuigi kui muutuja x on arusaadav, näiteks kui see on ainus sõltumatu muutuja võrrandis, jäetakse see allmärkus sageli välja.
Lineaarsete diferentsiaalvõrrandite väljendamiseks ja lahendamiseks on abiks Euleri notatsioon.
Tuletiste rakendamine matemaatikas
Tuletisi kasutatakse matemaatikas sageli. Nende abil saab määrata funktsiooni maksimumi või miinimumi, kõvera kallakut või isegi pöördepunkti.
Järgnevalt on toodud mõned juhud, kus me kasutame tuletist. Ja järgnevates osades käsitletakse igaüht neist väga üksikasjalikult. Tuletiste kasutamine toimub kõige sagedamini:
- Koguse muutumiskiiruse arvutamine
- Hea hinnangu saamine väärtuse kohta
- Kõvera puutuja ja normaalväärtuse võrrandi leidmine
- Pöördepunkti, maksimumi ja miinimumi kindlaksmääramine
- Kasvavate ja kahanevate funktsioonide hindamise tegemine
Tuletist kasutatakse murdepunkti, maksimumi ja miinimumi arvutamiseks.
Tuletisinstrumentide rakendamine reaalses elus
Tuletisi saab kasutada paljudes olukordades tegelikus elus. Siin on loetelu mõnest olukorrast, kus saab tuletisi kasutada:
- Ettevõtte kasumi ja kahjumi arvutamine.
- Temperatuuri kõikumise mõõtmiseks.
- Sõidukiiruse arvutamiseks, näiteks miili tunnis, kilomeeter tunnis jne.
- Derivaatide abil tuletatakse arvukalt füüsika võrrandeid.
- Maavärina suurusjärgu vahemiku leidmine on seismoloogiauuringute lemmikülesanne.
Kokkuvõte
- d2y/dx2 on teine tuletis.
- (dy/dx) ^2 on esimese tuletise ruut.
- Tuletist kasutatakse reaalses elus eri valdkondades mitmel eesmärgil.
- Tuletist kasutatakse matemaatikas maksimaalsete ja minimaalsete punktide arvutamiseks.
- Seda saab kasutada ettevõtluses ettevõtte finantside arvutamiseks ning kasumi ja kahjumi arvutamiseks.

