В чем разница между d2y/dx2=(dydx)^2? (Объяснение) - Все Различия
Оглавление
Производные имеют множество применений за пределами только математики и повседневной жизни, в том числе в таких предметах, как наука, инженерия, физика и другие.
Вы должны были освоить умение вычислять производную различных функций в предыдущих курсах, включая тригонометрические, неявные, логарифмы и т.д.
d2y/dx2 и (dydx)^2 - это два производных уравнения. Но чтобы понять их, сначала нужно понять, что именно является второй производной.
Производная функции в исчислении известна как вторая производная, иногда называемая производной второго порядка.
Вторая производная, грубо говоря, измеряет, как изменяется скорость изменения величины. Например, вторая производная положения объекта относительно времени - это мгновенное ускорение объекта или скорость, с которой изменяется скорость объекта относительно времени.
В этой статье я расскажу вам, в чем разница между d2y/dx2=(dydx)^2 и что именно означает производная.
D2y/dx2 Vs (dydx)^2
Производная от dy/dx (эти 2 могут выглядеть как индексные обозначения, но это не так). (dydx)2, с другой стороны, является квадратом первой производной.
Пример:
Возьмите Y=3 ???? 3+6 ???? 2y=3×3+6×2
Первая производная: dy/dx=9 ???? 2+12 ???? dydx=9×2+12x
Вторая производная: d2yd????2=18 ???? +12d2ydx2=18x+12
Квадрат первой производной: (dydx)2=(9 ???? 2+12 ???? )2=(81 ???? 4+216 ???? 3+144
Смотрите также: Континуум против Спектрума (подробное различие) - Все различияЧто такое вторая производная?
Когда вы дифференцируете производную, вы получаете вторую производную. Помните, что dy/dx - это производная y по отношению к x. Вторая производная, произносимая как "ди два y по d x в квадрате", представлена как d2y/dx2.
Природу стационарных точек легче выяснить с помощью второй производной (являются ли они точками максимума, минимума или точками перегиба).
Когда dy/dx = 0, кривая достигает стационарной точки. Тип стационарной точки (максимум, минимум или точка перегиба) может быть определен с помощью второй производной, как только будет установлено местоположение стационарной точки.
Смотрите также: В чем разница между линейной и экспоненциальной функциями? (Объяснение) - Все различия| d2y/d2x=Положительно | Это минимальная точка |
| d2y/d2x=отрицательно | Это максимальная точка |
| d2y/d2x равно нулю | Это и минимальная, и максимальная точка |
| d2y/d2x=0 | Проверьте значения dy/dx по обе стороны от стационарной точки, как и ранее в разделе стационарные точки |
Как определить точки максимума и минимума?

d2y/d2x - вторая производная.
Что такое дериватив?
Производная функции вещественной переменной в математике определяет чувствительность значения функции (выходного значения) к изменениям ее аргумента (входного значения). Основным инструментом исчисления является производная.
Скорость предмета, например, является производной его положения по времени. Она определяет, насколько быстро изменяется положение предмета с течением времени.
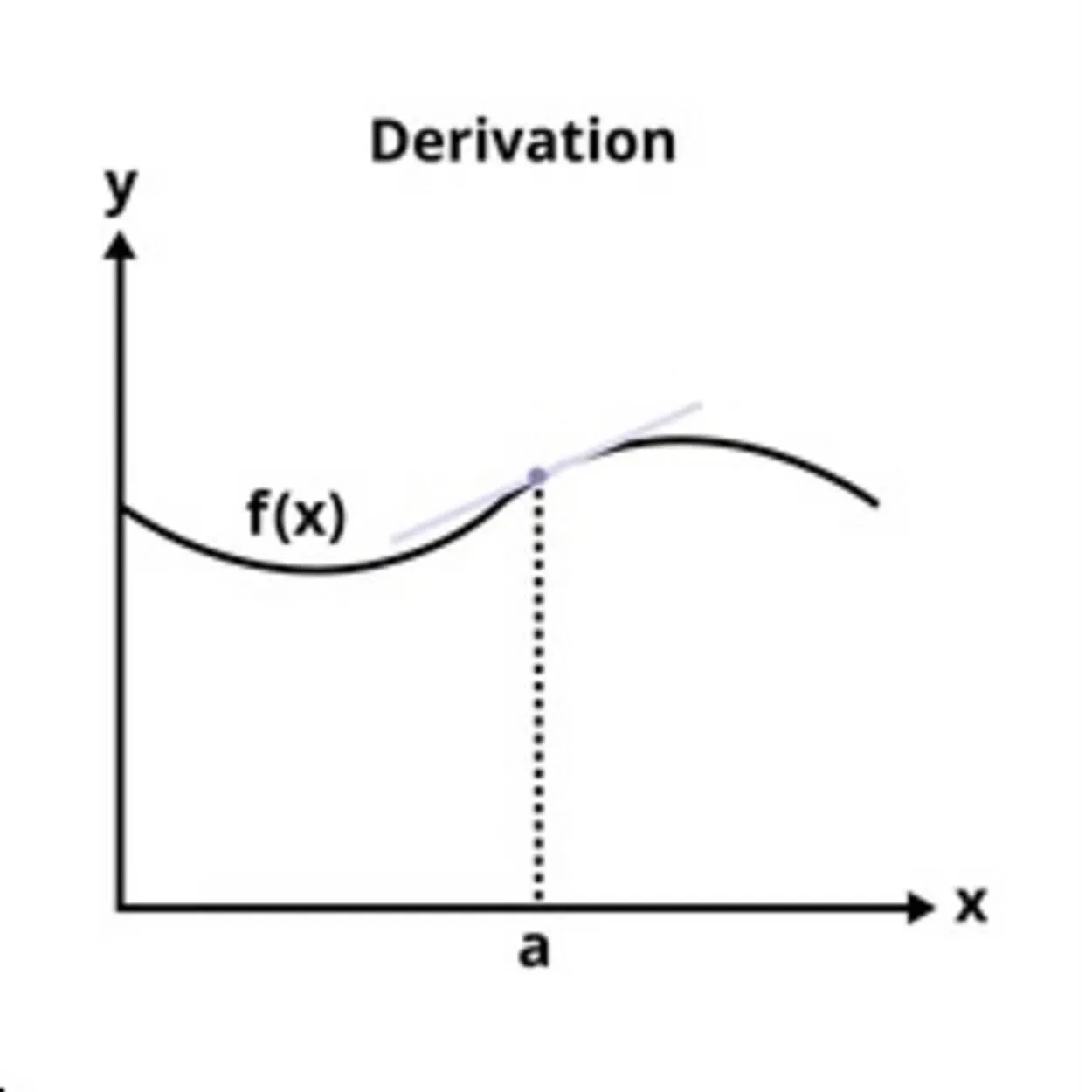
Когда это происходит, наклон касательной к графику функции при заданном входном значении является производной функции одной переменной. Функция, ближайшая к этому входному значению, лучше всего линейно аппроксимируется касательной линией.
Из-за этого производную часто называют "мгновенной скоростью изменения", которая представляет собой отношение мгновенного изменения зависимой переменной к изменению независимой переменной.
Для включения функций нескольких действительных переменных производные могут быть обобщены. Это обобщение переосмысливает производную как линейное преобразование, график которого после соответствующего перевода является наилучшим линейным приближением к графику исходной функции.
Что касается основы, обеспечиваемой выбором независимых и зависимых переменных, то матрица Якобиана - это матрица, которая представляет это линейное преобразование.
Он может быть вычислен с помощью частных производных независимых переменных. Вектор градиента заменяет матрицу Якобиана для вещественной функции с несколькими переменными.
Дифференцирование - это действие по нахождению производной. Антидифференцирование - это термин, обозначающий противоположный процесс. Антидифференцирование и интегрирование связаны в фундаментальной теореме исчисления. Две фундаментальные операции исчисления с одной переменной - это дифференцирование и интегрирование.
Посмотрите это видео, чтобы узнать о производных и функции действительной переменной
Различные обозначения
Нотация Лейбница
В 1675 году Готфрид Вильгельм Лейбниц ввел буквы dx, dy и dy/dx. Даже сегодня они часто используются, когда связь между зависимой и независимой переменными в уравнении y = f(x) считается функциональной.
Переменная для дифференцирования (в знаменателе) может быть задана с помощью нотации Лейбница, что важно для частичного дифференцирования.
обозначения Лагранжа
Одна из самых популярных современных нотаций дифференцирования, иногда известная как нотация прайма, использует знак прайма и приписывается Жозефу-Луи Лагранжу. Она обозначает производную функции f как f1.
Последнее обозначение обобщается и дает обозначение f(n) для n-й производной от f, что более удобно при обсуждении производной как функции, а не как функции самой себя, поскольку обозначение Лейбница может быть сложным в этой ситуации.
Условные обозначения Ньютона
В нотации дифференцирования Ньютона, часто известной как "точечная нотация", над именем функции ставится точка, чтобы обозначить производную по времени.
С помощью этой нотации представляются только производные по времени или длине дуги. Обычно она применяется для дифференциальных уравнений в дифференциальной геометрии и физике. Однако точечная нотация неприменима для нескольких независимых переменных и производных высокого порядка (порядка 4 и более).
Нотация Эйлера
Первая производная Df получается с помощью дифференциального оператора D в нотации Эйлера путем применения его к функции f. Dnd означает n-ую производную.
Если y = f(x) является зависимой переменной, то независимая переменная x часто уточняется добавлением подстрочного индекса x к D.
Хотя когда переменная x понятна, например, когда это единственная независимая переменная, содержащаяся в уравнении, этот подстрочный индекс часто опускают.
Для выражения и решения линейных дифференциальных уравнений удобно использовать нотацию Эйлера.
Применение производных в математике
Производные часто используются в математике. С их помощью можно определить максимум или минимум функции, наклон кривой или даже точку перегиба.
Ниже приведены несколько случаев, в которых мы будем использовать производную. И в следующих разделах мы подробно рассмотрим каждый из них. Применение производных чаще всего встречается в:
- Расчет скорости изменения величины
- Получение хорошей оценки стоимости
- Нахождение уравнения касательной и нормали кривой
- Определение точки перегиба, максимумов и минимумов
- Оценка возрастающей и убывающей функций
Производная используется для расчета точки перегиба, точки максимума и минимума
Применение деривативов в реальной жизни
Производные могут использоваться во многих ситуациях в реальной жизни. Вот список нескольких ситуаций, в которых вы можете использовать производные:
- Рассчитывать прибыль и убытки в бизнесе.
- Для измерения изменения температуры.
- Для расчета скорости движения, например, миль в час, километров в час и т.д.
- Многие уравнения физики выводятся с помощью производных.
- Нахождение диапазона магнитуд землетрясений - излюбленная задача в сейсмологических исследованиях.
Заключение
- d2y/dx2 - вторая производная.
- (dy/dx) ^2 - первая производная в квадрате.
- Производная используется в различных областях для различных целей в реальной жизни.
- Производная используется в математике для вычисления точек максимума и минимума.
- Его можно использовать в бизнесе для расчета финансов предприятия и подсчета прибыли и убытков.

